In this section, we discuss solubility equilibria that relate to some very commonly-encountered anions of metallic salts. These are especially pertinent to the kinds of separations that most college students are required to carry out (and understand!) in their first-year laboratory courses.
Solubility of oxides and hydroxides
Metallic oxides and hydroxides both form solutions containing OH– ions. For example, the solubilities of the [sparingly soluble] oxide and hydroxide of magnesium are represented by
Mg(OH)2(s) → Mg2+ + 2 OH– (10)
MgO(S) + H2O → Mg2+ + 2 OH– (11)
If you write out the solubility product expressions for these two reactions, you will see that they are identical in form and value.
Recall that pH = –log10[H+], so that [H+] = 10–pH.
One might naïvely expect that the dissolution of an oxide such as MgO would yield as one of its products the oxide ion O2+. But the oxide ion is such a strong base that it grabs a proton from water, forming two hydroxide ions instead:
O2+ + H2O → 2 OH–
This is an example of the rule that the hydroxide ion is the strongest base that can exist in aqueous solution. For more on this, see this explanation of the leveling rule for strong bases.
The fact that hydroxide ions are involved tells us that the solubility of these basic solids will depend on the pH. Hydrogen ions react with the hydroxides and oxides of metallic elements as expressed by the equations
Mg(OH)2 + 2 H+ → Mg2+ + 2 H2O (12)
MgO + 2 H+ → Mg2+ + H2O (13)
which have identical equilibrium constants that we denote by K's , the prime indicating that hydrogen ions are involved:
K's = [Mg2+] / [H+]2(14)
Because K's values are not commonly available, it is preferable to employ ordinary Ks data in dealing with problems involving the use of pH to control hydroxide solubility:
Using pH to separate metal hydroxides
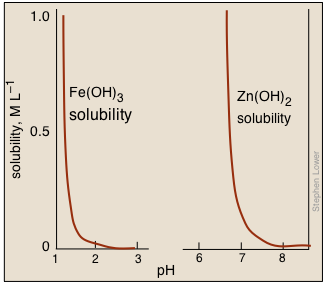
Metal hydroxides having widely different solubilities can often be used to precipitate one metal cation while leaving the other in solution, thus affording a convenient means of separating a mixture of two such cations. For example, Fe(III) can be selectively be removed from Zn(II) by adjusting the pH appropriately.
Bear in mind that many metal hydroxides are amphoteric, so raising the pH too far can cause the metal ions to re-dissolve. The aluminum ion is a commonly-encountered example. Although the hydroxide will precipitate over a fairly wide range of pH, it will also dissolve in strongly basic solutions to form the aluminate ion:
Al(OH)3(s) + OH– → Al(OH)4–(aq)
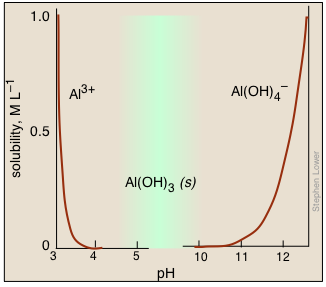
Thus if we add a small quantity of sodium hydroxide to a solution of Al3+, we first see a white gelatinous precipitate of Al(OH)3 form. Continued addition of this strong base eventually raises the pH to the point where the precipitate dissolves.
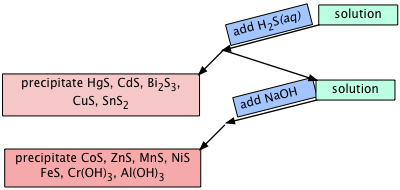
Solubility of sulfides
The sulfides of transition metals are generally insoluble in water, and these metals have long been separated from other ions by bubbling hydrogen sulfide gas through a solution of the metal cations.
Fe2+ + H2S(aq) → FeS(s) + 2 H–
The great utility of these precipitation reactions resulted in the compilation of a long list of solubility products of the form
[Fe2+][S2–] = 5 × 10–18
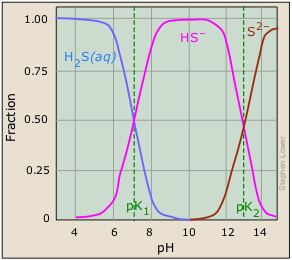
This very readable article by Rollie Meyers of UC-Berkeley is titled The New Low Value the Second Dissociation Constant for H2S: Its History, Its Best Value, and Its Impact on the Teaching of Science: J Chem Educ 1986: (8) 687-690.
There is no doubt that this works, but it turns out that the explanation of why it works was completely wrong! In 1986, it was found that pK2 (the pH at which the sulfur in an H2S solution is equally divided between HS– and S2–) is not 13 as indicated in the plot, but is around 19. This means that even at the highest attainable pH (about 14), the concentration of S2– is negligible!
It is now understood that the situation is very similar to the one we described above for the dissolution of oxides. The sulfide ion, like the oxide ion, is too strong a base to exist in water:
(Teachers take note; what you have likely been teaching is wrong!)
S2– + H2O → HS– + OH–
so the dissolution of FeS, for example, is properly described b
FeS(s) + H2O → Fe2+ + OH– + HS–
and its solubility product is
Ks = [Fe2+][OH–][HS–] = 600
So what difference is all this supposed to make to you?
Very little, really! Instead of the Ks values for transition metal sulfides ranging from about 10–54 to 10–10 (as many textbooks still tell you), the "true" values go from 10–33 to 10+10 — still a respectable range. And in acidic solution, both the [OH–] and [HS–] values are so low that precipitation of the more insoluble sulfides is favored. So if you are carrying out sulfide precipitations in the lab, nothing in your procedure is changed.
The more important lesson to be learned is perhaps that this is the way science advances: what we believed and made students learn for nearly a century can be subject to revision by the careful work of a few individuals who are motivated to question "what everyone knows".
Some solubility-related health problems
Chemistry of tooth decay
Did you know? Dogs are less subject to tooth decay because their saliva is more alkaline.
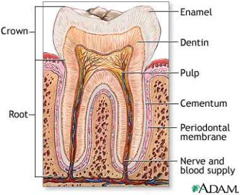
The “hard” components of our bodies — bones and teeth — are made so by a modified form of calcium phosphate known as calcium hydroxyphosphate,
Ca5(PO4)3OH, commonly known as hydroxylapatite (the apatites are a large family of naturally-occurring calcium phosphate minerals .)
Bone is a composite material consisting of about equal amounts of hard hydroxylapatite crystals embedded in a collagen protein matrix. Teeth, particularly the outer enamel coatings, are almost entirely hydroxylapatite, but protein material plays a crucial role in shaping and elongating the crystalline nanostructure to make the enamel much stronger than bonelink.
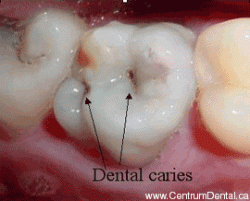
Although ordinary Ca3(PO4)2 is insoluble in water and dilute acid, the -OH group in hydroxylapatite makes tooth enamel vulnerable to dissolution by acids, including the weak organic acids produced when oral bacteria metabolize food carbohydrates, giving rise to dental caries.
Ca5(PO4)3OH(s) + H+ → Ca5(PO4)3+(aq) + H2O
This acid attack begins very quickly during a meal when food materials adhere to the teeth. Saliva, which is slightly alkaline and contains several antibacterial agents, is the body's natural defense against tooth decay; its alkalinity helps restore the enamel by supplying hydroxide ions to the Ca5(PO4)3+ decay product. This works best, of course, when one brushes and flosses after meals, and avoids frequent snacks between meals.
Fluoride ion treatment has long been known to reduce tooth decay. These ions replace the -OH group in dissolved enamel, converting it to fluoroapatite:
Ca5(PO4)3++ F– → Ca5(PO4)3F(s)
which is actually more resistant to dissolution by acids than is the original hydroxylapatite.
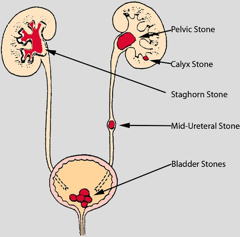
Chemistry of kidney stones
These are crystalline aggregates that can form when the urine becomes supersaturated in a slightly-soluble substance. The most common of these is calcium oxalate Ca(COO)2, but uric acid, calcium phosphate, and several other agents can also form stones, which are known medically as renal calculi.
Stones formed in a kidney can remain there, often without causing any discomfort. But if they migrate into a ureter (the narrow tubes that lead to the bladder) they tend to lodge there and impede flow of urine into the bladder. The resulting buildup of pressure as the kidney continues to produce urine swells the kidney and ureter, giving rise to intensely painful spasms. The increased pressure usually helps move the stones along into the bladder, from which they can be excreted with the urine.
The root causes of kidney stones are complex and not thoroughly understood, but it is known that the best way to minimize their occurrence is to keep the urine as dilute as possible by drinking plenty of water. Individuals who are subject to calcium oxalate stones should avoid foods such as rhubarb and spinach that have a high oxalate content. Black tea also contains significant amounts of oxalates. Other teas such as green tea and rooibos have much lower oxalate levels, and there is some evidence that these can reduce the incidence of stones.
Carbonate solids, mostly in the form of limestones, cover seven percent of the world's land surface.
Solubility of carbonates
Most carbonates are slightly soluble in water. The dissolution of calcium carbonate (calcite), which we will use as an example in this section, is typical:
[Ca2+][CO32–] = 2.8 × 10–9
But Ks expressions such as this are of limited use in dealing with carbonate solids because they fail to capture the following facts:
- Being salts of a weak acid (carbonic acid H2CO3), carbonates have solubilities that depend on the pH.
- The diprotic nature of carbonic acid adds a significant complication because the distribution of its dissociation products HCO3– and CO32– is itself a function of pH.
- If the system is in equilibrium with the atmosphere (in which the partial pressure of CO2 is 10–3.5 atm), the potential availability this huge reservoir adds another twist. For many purposes, one can get around this by assuming a "closed system" or that equilibration is too slow to affect a given process.
- As if this were not enough, a final complication is that solid bicarbonates of Group 2 and higher metals do not exist. This means that a solution saturated with HCO3– is in equilibrium with a carbonate (not bicarbonate) solid. Weird!
The quantitative solution of a carbonate-solubility problem for something like CaCO3 is not a trivial task. Because there are six concentration variables
(for H2CO3, H2CO3–, CO32–, Ca2+, H+ and OH–), one must set up and solve six simultaneous equations expressing the relationships between them. In practice, one usually makes approximations that allow the use of graphical methods as described on this carbonate equilibria page. But this is advanced stuff that is way beyond the scope of this course.
Nevertheless, the carbonate system is so important in shaping our world that even a qualitative overview of it is an essential part of what you should expect to get out of introductory general chemistry. We will make it easier for you by focusing on the general concepts rather than on numerical problems, and presenting some of the results without dragging you through the derivations.
The carbonate system and geochemistry
Carbon is unique in that is the only element that is transported in significant quantities between the atmosphere, hydrosphere, and lithosphere as part of the global biogeochemical cycle.
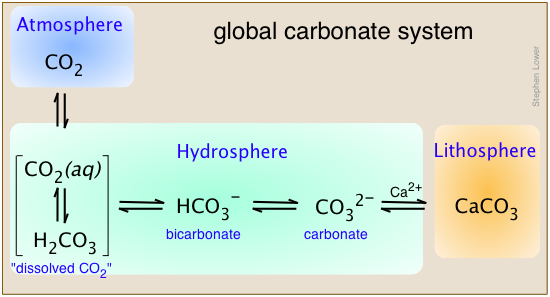
This diagram shows the principal carbonate species that constitute the global system, using calcium as the example metal. Note that in aqueous solution, "dissolved CO2" is an equilibrium mixture of hydrated CO2 molecules and carbonic acid. To keep things as simple as possible, we will not distinguish between them in what follows, and just use the formula H2CO3 to represent the two species collectively.
The other Group 2 metals, especially Mg, along with iron and several other transition elements are also found in carbonate sediments.
When rain falls through the air, it absorbs atmospheric carbon dioxide, a small portion of which reacts with the water to form carbonic acid. Thus all pure water in contact with the air becomes acidic, eventually reaching a pH of 5.6.
As noted above, the equilibrium between bicarbonate and carbonate ions depends on the pH. Since the pH scale is logarithmic, it makes sense (and greatly simplifies the construction of the plot) to employ a log scale for the concentrations. The plot shown below corresponds to a total carbonate-system concentration of 10–3 M, which is representative of many ground waters. For river and lake waters, 10–5 M would be more typical; this would simply shift the curves downward without affecting their shapes.
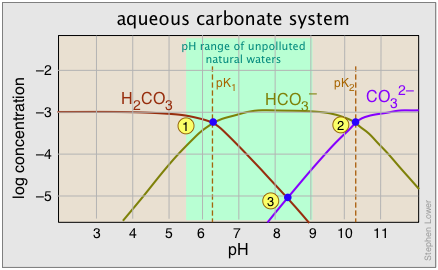
A 10–3 M solution of sodium bicarbonate would have a pH denoted by point 3, with [H2CO3] and [CO32–] constituting only 1% (10–5 M) of the system. This corresponds to the equilibrium
2 HCO3– → H2CO3 + CO32–
Carbonates act as bases and, as such, react with acids. Thus, the portion of the global water cycle that transports carbon from the air into natural waters constitutes a gigantic acid-base reaction that yields hydrogen carbonate ions, commonly referred to as bicarbonate. The natural waters that result have pH values between 6 and 10 and are essentially solutions of bicarbonates.
Limestone caves and sinkholes
Stalactites are the ones hanging down from the ceilings; a useful mnemonic is to note that both "ceiling" and "stalactite" contain the letter "c".
When rainwater permeates into the soil, it can become even more acidic owing to the additional CO2 produced by soil organisms. Also, the deeper the water penetrates, the greater its hydrostatic pressure and the more CO2 it can hold, further increasing its acidity. If this water then works its way down through the fissures and cracks within a limestone layer, it will dissolve some of limestone, leaving void spaces which may eventually grow into limestone caves or form sinkholes that can swallow up cars or houses.
A well-known feature of limestone caves is the precipitated carbonate formations that decorate the ceilings and floors. These are known as stalactites and stalagmites, respectively.
When water emerges from the ceiling of a cave that is open to the atmosphere, some of the excess CO2 it contains is released as it equilibrates with the air. This raises its pH and thus reduces the solubility of of the carbonates, which precipitate as stalactites.
Some of the water remains supersaturated and does not precipitate until it drips to the cave floor, where it builds up the stalagmite formations.
Hard water
For more on hard water, see Steve's Hard Water page, or this Wikipedia page.
This term refers to waters that, through contact with rocks and sediments in lakes, streams, and especially in soils (groundwaters), have acquired metallic cations such as Ca2+, Mg2+, Fe2+, Fe3+, Zn2+ Mn2+, etc. Owing to the ubiquity of carbonate sediments, the compensating negative charge is frequently supplied by the bicarbonate ion HCO3–, but other anions such as SO42–, F–, Cl–, PO43– and SiO42– may also be significant.
Solid bicarbonates are formed only by Group 1 cations and all are readily soluble in water. But because HCO3– is amphiprotic, it can react with itself to yield carbonate:
2 HCO3– → H2O + CO32– + CO2(g)
If bicarbonate-containing water is boiled, the CO2 is driven off, and the equilibrium shifts to the right, causing any Ca2+ or similar ions to form a cloudy precipitate. If this succeeds in removing the "hardness cations", the water has been "softened". Such water is said to possess carbonate hardness, sometimes known as "temporary hardness".
Waters in which anions other than HCO3– predominate cannot be softened by boiling, and thus possess non-carbonate hardness or "permanent hardness".
Hard waters present several kinds of problems, both in domestic and industrial settings:
- Waters containing dissolved salts leave solid deposits when they evaporate. Residents of areas having hard water (about 85 percent of the U.S.) notice evaporative deposits on shower walls, in teakettles, and on newly-washed windows, glassware, and vehicles.
- Much more seriously from an economic standpoint, evaporation of water in boilers used for the production of industrial steam leaves coatings on the heat exchanger surfaces that impede the transfer of heat from the combustion chamber, reducing the thermal transfer efficiency. The resultant overheating of these surfaces can lead to their rupture, and in the case of high-pressure boilers, to disastrous explosions. In the case of calcium and magnesium carbonates, the process is exacerbated by the reduced solubility of these salts at high temperatures. Removal of boiler scales is difficult and expensive.
Municipal water supplies in hard-water areas tend to be supersaturated in hardness ions. As this water flows through distribution pipes and the plumbing of buildings, these ions often tend to precipitate out on their interior surfaces. Eventually, this scale layer can become thick enough to restrict or even block the flow of water through the pipes. When scale deposits within appliances such as dishwashers and washing machines, it can severely degrade their performance. - Cations of Group 2 and above react with soaps, which are sodium salts of fatty acids such as stearic acid, C17H35COOH. The sodium salts of such acids are soluble in water, which allows them to dissociate and act as surfactants:
C17H35COONa → C17H35COO– Na+
but the presence of polyvalent ions causes them to form precipitates
2 C17H35COO– + Ca2+ → (C17H35COO–)2Ca(s)
Calcium stearate is less dense than water, so it forms a scum that floats on top of the water surface; anyone who lives in a hard-water area is likely familiar with the unsightly "bathtub rings" it leaves around the high-water mark or the shower-wall stains.
The material discussed in this section is not ordinarily covered in first-year General Chemistry courses. But not because it's not interesting...
All heterogeneous equilibria, on close examination, are beset with complications. But solubility equilibria are somewhat special in that there are more of them. Back in the days when the principal reason for teaching about solubility equilibria was to prepare chemists to separate ions in quantitative analysis procedures, these problems could be mostly ignored. But now that the chemistry of the environment has grown in importance — especially that relating to the ocean and natural waters — there is more reason for chemical scientists to at least know about the limitations of simple solubility products. This section will offer a quick survey of the most important of these complications, while leaving their detailed treatment to more advanced courses.
Tabulated Ks values are notoriously unreliable
Many of the Ks values found in tables were determined prior to 1940 (some go back to the 1880s!) at a time before highly accurate methods became available. Especially suspect are many of those for highly insoluble salts which are more difficult to measure.
A table showing the variations in Ks values for the same salts among ten textbooks was published by Clark and Bonikamp in J Chem Educ. 1998 75(9) 1183-85.
A good example that used a variety of modern techniques to measure the solubility of silver chromate was published by A.L. Jones et al in the Australian J. of Chemistry, 1971 24 2005-12.
Generations of chemistry students have amused themselves by comparing the disparate Ks values to be found in various textbooks and tables. In some cases, they differ by orders of magnitude. There are several reasons for this in addition to the ones described in detail further on.
- The most direct methods of measuring solubilities (that we discussed above) tend to not be very accurate for sparingly soluble salts. Two-significant figure precision is about the best one can hope for in a single measurement.
- Many insoluble salts can exist in more than one crystalline form (polymorphs), and in some cases also as amorphous solids. Precipitation under different conditions (in the presence of different ions, at different temperatures, etc.) can yield different or mixed polymorphs.
- Other ions present in the solution can often get incorporated into the crystalline solid, usually replacing an ion of similar size (substitutional solid solutions). When this happens, it is no longer valid to write the equilibrium condition as a simple "product". This is very common in mineral deposits, and an important consideration in geochemistry.
Most salts are not completely dissociated in water
The dissolution of cadmium iodide is water is commonly represented as
CdI2(s) → Cd2+ + 2 I–
To most students (and to most of their teachers!), this would imply that a 0.1M solution of this salt would contain 0.1M of Cd2+(aq) — and this would be seriously in error because it fails to take into account that the two ions react with each other.
Firstly, they combine to form neutral, largely-covalent molecular species:
Cd2+(aq) + 2 I–(aq) → CdI2(aq)
This non-ionic form accounts for 78 percent of the Cd present in the solution!
In addition, they form a molecular ion CdI–(aq) according to the following scheme:
The data shown here and in the table below are taken from the article Salts are Mostly NOT Ionized by Stephen Hawkes: 1996 J Chem Educ. 73(5) 421-423. Every Chemistry teacher should read this!
This fact was stated by Arrhenius in 1887, but has been largely ignored and is almost never mentioned in standard textbooks.
| CdI2(s) → Cd2+ + 2 I– | K1 = 10–3.9 |
| Cd2+ + I– → CdI+ | K2= 10+2.3 |
| CdI2(s) → CdI++ I– | K = 10–1.6 = 0.023 |
As a consequence, the concentration of "free" Cd2+(aq) in an aqueous cadmium iodide solution is only about 2% of the value you would calculate by taking K1 as the solubility product. The principal component of such as solution is actually [covalently-bound] CdI2(aq).
It turns out that many salts, especially those of metals beyond Group 2, are similarly only partially ionized in aqueous solution:
| salt | molarity | % cation | other species |
|---|---|---|---|
| KCl | 0.52 | 95 | KCl(aq) 5% |
| MgSO4 | 0.04 | 58 | MgSO4(aq) 42% |
| CaCl2 | 0.44 | 70 | CaCl+(aq) 30% |
| CuSO4 | 0.045 | 56 | CuSO4(aq) 44% |
| CdI2 | 0.50 | 2 | CdI2(aq) 76%, CdI–(aq) 22% |
| FeCl3 | 0.1 | 10 | FeCl2+(aq) 42%, FeCl2(aq) 40%, FeOH2+(aq) 6%, Fe(OH)2+(aq) 2% |
So what is the student supposed to make of all this?
If you are enrolled in an introductory course and don't plan on taking more advanced courses in chemistry or biochemistry, you can probably be safe in ignoring this, since your instructor and textbook likely do so.
But if you expect to do more advanced work or teach, you really should take note of these points, since few textbooks mention them.
Formation of hydrous complexes
Transition metal ions form a large variety of complexes with H2O and OH–, both of which have electron-pairs available to coordinate with the central ion. This gives rise to a large variety of soluble species that are in competition with an insoluble solid. Because of this, a single equilibrium constant (solubility product) cannot describe the behavior of a solid such as Fe(OH)3, which we summarize here as an example.
Aquo complexes The electrostatic field of the positively-charged metal ion enhances the acidic nature of these H2O molecules, encouraging them to shed a proton and leaving OH– groups in their place.
Fe(H2O)63+ → Fe(H2O)5(OH)2++H+
This is just the first of a series of similar reactions, each one having a successively smaller equilibrium constant:
Fe(H2O)5(OH)2+→ Fe(H2O)4(OH)2+→ Fe(H2O)3(OH)3o → Fe(H2O)2(OH)4–
Hydroxo complexes But there's more: when the hydroxide ion acts as a ligand, it gives rise to a series of hydroxo complexes, of which the insoluble Fe(OH)3 can be considered a member:
| Fe3+ + 3 OH– → Fe(OH)3(s) | 1/Ks = 1038 |
| Fe3+ + H2O → Fe(OH)2+ + H+ | K = 10–2.2 |
| Fe3+ + 2H2O → FeOH+ + 2H+ | K = 10–6.7 |
| Fe3+ + 4H2O → Fe(OH)4– + 4H+ | K = 10–23 |
| 2Fe3+ + 2H2O → Fe2(OH)24+ + 2H+ | K = 10–2.8 |
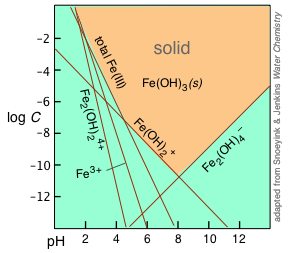
Because five equilibria are involved in the hydroxy-complex behavior alone, a complete treatment of this system for Fe3+ requires the solution of five simultaneous equations, which is not a lot of fun. Fortunately, it is possible to make some approximations which greatly simplify the construction of a log-concentration vs. pH plot as shown above.
The equilibria listed above all involve H+ and OH– ions, and are therefore pH dependent, as illustrated by the straight lines in the plot, whose slopes reflect the pH dependence of the corresponding ionic species. At any given pH, the equilibrium with solid Fe(OH)3 is controlled by the ionic species having the highest concentration at any given pH. The corresponding lines in the plot therefore delineate the region (indicated by the orange shading) at which the solid can exist.
Ionic interactions: the "non-common ion effect"
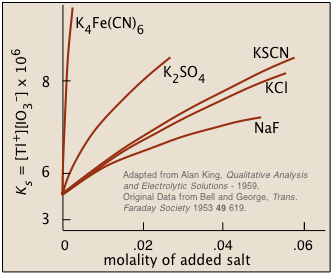
Solubility of thallium iodate
in solutions containing dissolved salts→
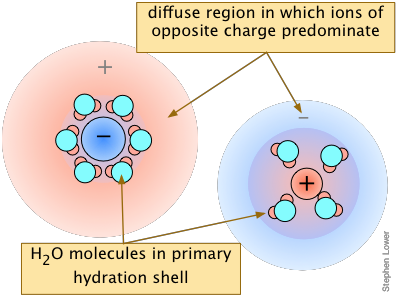
The overall effect is to reduce the concentrations of the less-shielded ions that are available to combine to form a precipitate. We say that the thermodynamically-effective concentrations of these ions are less than their "analytical" concentrations. Chemists refer to these effective concentrations as ionic activities, and they denote them by curly brackets {Ag+} as opposed to square brackets [Ag+] which refer to the nominal or analytical concentrations.
Some examples of solubility calculations that take ionic activities into account can be seen at this Utah State U. site.
Although the concentrations of ions in equilibrium with a sparingly soluble solid are so low that they are essentially the same as the activities, the presence of other ions at concentrations of about 0.001M or greater can materially reduce the activities of the dissolution products, permitting the solubilities to be greater than what simple equilibrium calculations would predict.
Measured solubilities are averages and depend on size
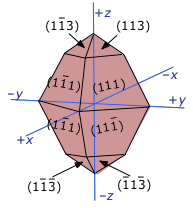
And because many salts can exhibit different external shapes depending on the conditions under which they are formed, solubility products are similarly dependent on these conditions.
Very small crystals are more soluble than big ones
Molecules or ions that are situated on edges or corners are less strongly bound to the remainder of the solid than those on plane surfaces, and will consequently tend to dissolve more readily.
Thus the leftmost face in the schematic lattice below will have more edge-bound molecular units than the other two, and this face (11) will be more soluble.
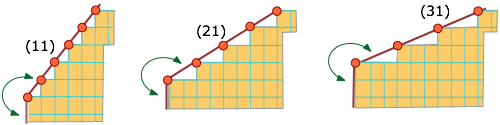
This means, among other things, that smaller crystals, in which the ratio of edges and corners is greater, will tend to have greater Ks values than larger ones. As a consequence, smaller crystals will tend to disappear in favor of larger ones.
Practical use is sometimes made of this when the precipitate initially formed in a chemical analysis or separation is too fine to be removed by filtration. The suspension is held at a high temperature for several hours, during with time the crystallites grow in size. This procedure is sometimes referred to as digestion.
Why do supersaturated solutions form?
Another common misunderstanding!
Contrary to what you may have been taught, precipitates do not form when the ion concentration product reaches the solubility product of a salt in a solution that is pure and initially unsaturated; to form a precipitate from a homogeneous solution, a certain degree of supersaturation is required.
The extent of supersaturation required to initiate precipitation can be surprisingly great. Thus formation of barium sulfate BaSO4 by combining the two kinds of ions does not occur until Qs exceeds Ks by a factor of 160 or more.
In part, this reflects the fact that precipitation proceeds by a series of reactions beginning with formation of an ion-pair which eventually becomes an ion cluster:
Ba2+ + SO42– → (BaSO4)0 → (BaSO4)20 → (BaSO4)30 → etc.
Owing to their overall neutrality, these aggregates are not stabilized by hydration, so they are more likely to break up than not. But a few may eventually survive until they are large enough (but still submicroscopic in size) to serve as precipitation nuclei.
Many substances other than salts form supersaturated solutions, and some salts form them more readily than others. Supersaturated solutions are easily made by dissolving the solid to near its solubility limit in a warmed solvent, and then letting it cool.
Supersaturated solutions are not in equilibrium (Qs > Ks) and are inherently unstable; dropping a "seed" crystal of the solid into such a solution will usually initiate rapid precipitation. But as is explained below, even a tiny dust particle may be enough. An old chemist's trick is to use the tip of a glass stirring rod to scrape the inner surface of a container holding a supersaturated solution; the minute particles of glass that are released presumably serve as precipitation nuclei.
The nucleation problem: precipitation is [theoretically] impossible!
For more on nucleation as it pertains to the boiling and condensation of liquids, see this discussion of bubbles, drops, and superheating.
Any process in which a new phase forms within an existing homogeneous phase is beset by the nucleation problem: the smallest of these new phases — raindrops forming in air, tiny bubbles forming in a liquid at its boiling point — are inherently less stable than larger ones, and therefore tend to disappear. The same is true of precipitate formation: if smaller crystals are more soluble, then how can the tiniest, first crystal, form at all?
In any ionic solution, small clumps of oppositely-charged ions are continually forming by ordinary collisional processes. The smallest of these aggregates possess a higher free energy than the isolated solvated ions, and they rapidly dissociate. Occasionally, however, one of these proto-crystallites reaches a critical size whose stability allows it to remain intact long enough to serve as a surface (a "nucleus") onto which the deposition of additional ions can lead to still greater stability. At this point, the process passes from the nucleation to the growth stage.
Theoretical calculations predict that nucleation from a perfectly homogeneous solution is a rather unlikely process; tenfold supersaturation should produce only one nucleus per cm3 per year. Most nucleation is therefore believed to occur heterogeneously on the surface of some other particle, possibly a dust particle. The efficiency of this process is critically dependent on the nature and condition of the surface that gives rise to the nucleus.
Some interesting examples and applications
- You can make a saturated solution of sodium acetate trihydrate,
CH3COONa·3H2O, without adding any water at all. On heating the solid to
97° C, it dissolves in its own water of hydration. 
If you let a supersaturated sodium acetate solution cool to room temperature and then seed it with a crystal of the solid, you will notice that the test tube becomes warm: crystallization is usually an exothermic process. Advantage is taken of this in some types of hand warmers in which a metal activating strip initiates crystallization as described here. On a much larger scale, supersaturated solutions can be used to store thermal energy — for example, from solar panels that absorb heat during the day, into a reservoir from which heat can be extracted during the night.
Sometimes we want solutions to remain supersaturated. A good example is liquid honey, which is essentially a supersaturated solution of sugar in water. You may have noticed that after it has been stored for some time in your kitchen cupboard, it turns into a sticky crystalline paste. The same thing can happen to some sweet syrups. This is easily corrected by heating it in a pan of hot water.- City water treatment authorities commonly try to maintain a slight supersaturation of carbonates in order to produce a thin coating of scale deposits within distribution pipes in order to protect them from corrosion.
- The upper parts of the ocean are mostly supersaturated in calcium carbonate. For the more than 105 different species of protozoans known as foraminifera, this is of considerable importance because their outer skeletal parts are composed of CaCO3 which would dissolve away in the absence of this supersaturation.
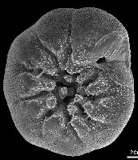As these organisms die, they sink to the bottom of the ocean and deposit CaCO3 on the ocean floor. Tectonic forces eventually return these deposits to the surface where they form extensive limestone deposits which constitute the major carbon repository in the global carbon cycle. Most of the North American limestone deposits result from the evaporation of ancient seas.
The solubility of calcium carbonate increases with pressure, so in the deeper Pacific ocean, the skeletons dissolve before they reach the bottom, where silica-based deposits (from other organisms) cover the floor.
