You may recall that in the earlier unit on phase equilibria, we pointed out that aggregations of molecules that are more disordered tend to be the ones that are favored at higher temperature, whereas those that possess the lowest potential energy are favored at lower temperatures. This is a general principle that applies throughout the world of matter; the stable form at any given temperature will always be that which leads to the best balance between low potential energy and high molecular disorder.
To see how these considerations are applied to solutions, think about the individual steps that must be carried out when a solute is dissolved in a solvent:
| 1 If the solute is a solid or liquid, it must first be dispersed — that is, its molecular units must be pulled apart. This requires energy, and so this step always works against solution formation. |
endothermic |
| 2 The solute must then be introduced into the solvent. Whether this is energetically favorable or unfavorable depends on the nature of the solute and solvent. If the solute is A and the solvent is B, then what is important is the strength of the attractive forces between A-A and B-B molecules, compared to those between A-B pairs; if the latter are greater, then the potential energy will be lower when the substances are mixed and solution formation will be favored. |
Exothermic if A-B attractions stronger than A-A + B-B Endothermic if attractions between like molecules are stronger than those between unlike molecules. |
If step 2 releases more energy than is consumed in step 1, this will favor solution formation, and we can generally expect the solute to be soluble in the solvent. Even if the dissolution process is slightly endothermic, there is a third important factor, the entropy increase, that will very often favor the dissolved state.
Entropy of dissolution
As anyone who has shuffled a deck of cards knows, disordered arrangements of objects are statistically more favored simply because there are more ways in which they can be realized. And as the number of objects increases, the more does statistics govern their most likely arrangements. The numbers of objects (molecules) we deal with in Chemistry is so huge that their tendency to become as spread out as possible becomes overwhelming. But in doing so, the thermal energy they carry with them is also spread and dispersed, so the availability of this energy, as measured by the temperature, is also of importance. Chemists use the term "entropy" to denote this aspect of molecular randomness.
Readers of this section who have had some exposure to thermodynamics will know that solubility, like all equilibria, is governed by the Gibbs free energy change for the process, which incorporates the entropy change at a fundamental level. This topic is treated in some detail in the unit on the Thermodynamics of Equilibrium.
A proper understanding of these considerations requires some familiarity with thermodynamics, which most students do not encounter until well into their second semester of Chemistry (see box at left). If you are not there yet, don't despair; you are hereby granted temporary permission to think of molecular "disorder" and entropy simply in terms of "spread-outedness".
Thus in the very common case in which a small quantity of solid or liquid dissolves in a much larger volume of solvent, the solute becomes more spread out in space, and the number of equivalent ways in which the solute can be distributed within this volume is greatly increased. This is the same as saying that the entropy of the solute increases.
If the energetics of dissolution are favorable, this increase in entropy means that the conditions for solubility will always be met. Even if the energetics are slightly endothermic the entropy effect can still allow the solution to form, although perhaps limiting the maximum concentration that can be achieved.
In such a case, we may describe the solute as being slightly soluble in a certain solvent. What this means is that a greater volume of solvent will be required to completely dissolve a given mass of solute.
"Like dissolves like"
Polar and non polar molecules
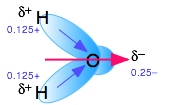Polar molecules are those in which electric charge is distributed asymmetrically. The most familiar example is ordinary water, in which the highly electronegative oxygen atom pulls part of the electric charge cloud associated with each O–H bond closer to itself. Although the H2O molecule is electrically neutral overall, this charge imbalance gives rise to a permanent electric dipole moment.
"Associated" liquids
Chemists use this term to refer to liquids in which the effects of hydrogen bonding dominate the local structure. Water is the most important of these, but ammonia NH3 and hydrogen cyanide HCN are other common examples.
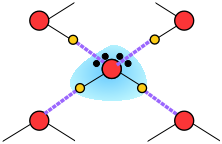Thus liquid water consists of an extended network of H2O molecules linked together by dipole-dipole attractions that we call hydrogen bonds. Because these are much weaker than ordinary chemical bonds, they are continually being disrupted by thermal forces. As a result, the extended structure is highly disordered (in contrast to that of solid ice) and continually changing.
When a solute molecule is introduced into an associated liquid, a certain amount of energy must be expended in order to break the local hydrogen-bond structure and make space for the new molecule. If the solute is itself an ion or a polar molecule, new ion-dipole or dipole-dipole attractions come into play. In favorable cases these may release sufficient potential energy to largely compensate for the energy required to incorporate the solute into the structure.
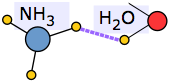An extreme example of this occurs when ammonia dissolves in water. Each NH3 molecule can form three hydrogen bonds, so the resulting solution is even more hydrogen-bonded than is pure water — accounting for the considerable amount of heat released in the process and the extraordinarily large solubility of ammonia in water.
Non polar solutes are sparingly soluble in water
When a non polar solute such as oxygen or hexane is introduced into an associated liquid, we might expect that the energy required to break the hydrogen bonds to make space for the new molecule is not compensated by the formation of new attractive interactions, suggesting that the process will be energetically unfavorable.
We can therefore predict that solutes of these kinds will be only sparingly soluble in water, and this is indeed the case.
The hydrophobic effect
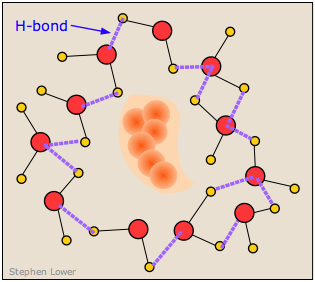It turns out, however, that this is not an entirely correct explanation for the small solubility of non polar solutes in water. It is now known that the H2O molecules that surround a non polar intruder and find themselves unable to form energy-lowering polar or hydrogen-bonded interactions with it will rearrange themselves into a configuration that maximizes the hydrogen bonding between the water molecules themselves. In doing so, this creates a cage-like shell around the solute molecule. In terms of the energetics of the process, these new H2O-H2O interactions largely compensate for the lack of solute-H2O interactions.
But this shell of highly organized water molecules exacts its own toll on the solubility by reducing the entropy of the system. Dissolution of a solute normally increases the entropy by spreading the solute molecules (and the thermal energy they contain) through the larger volume of the solvent. But in this case, the H2O molecules within the highly structured shell surrounding the solute molecule are themselves constrained to this location, and their number is sufficiently great to reduce the entropy by far more than the dissolved solute increases it.
The small solubility of a non polar solute in an associated liquid such as water results more from the negative entropy change rather than from energetic considerations. This phenomenon is known as the hydrophobic effect.
In the next section, we will explore the ways in which these energy-and-entropy considerations come together in various kinds of solutions.
Gaseous solutions
Mixtures of gases are really solutions, but we tend not to think of them this way because they mix together freely and with no limits to their compositions; we say that gases are miscible in all proportions.
For a [non-mathematical!] thermodynamic description of why gases spontaneously expand and mix, see here.
To the extent that gases behave ideally (because they consist mostly of empty space), their mixing does not involve energy changes at all; the mixing of gases is driven entirely by the increase in entropy (S) as each kind of molecule occupies and shares the space and kinetic energy of the other. (Recall Dalton's law: "Every gas is a vacuum to every other gas.")
Your nose can be a remarkably sensitive instrument for detecting components of gaseous solutions, even at the parts-per-million level. The olfactory experiences resulting from cooking cabbage, eating asparagus, and bodily emanations that are not mentionable in polite society are well known.
See this list of odor thresholds.
Can solids or liquids "dissolve" in a gaseous solvent? In a very narrow sense they can, but only to a very small extent. Dissolution of a condensed phase of matter into a gas is formally equivalent to evaporation (of a liquid) or sublimation (of a solid), so the process really amounts to the mixing of gases.
The energy required to remove molecules from their neighbors in a liquid or solid and into the gaseous phase is generally too great to be compensated by the greater entropy they enjoy in the larger volume of the mixture, so solids tend to have relatively low vapor pressures. The same is true of liquids at temperatures well below their boiling points.
These two cases of gaseous solutions can be summarized as follows:
| gaseous solvent, solute → | gas | liquid or solid |
|---|---|---|
| energy to disperse solute | nil | large |
| energy to introduce into gas | nil | nil |
| increase in entropy | large | large |
| miscibility | complete | very limited |
Solutions of gases in liquids
Gases dissolve in liquids, but usually only to a small extent.
When a gas dissolves in a liquid, the ability of the gas molecules to move freely throughout the volume of the solvent is greatly restricted. If this latter volume is small, as is often the case, the gas is effectively being compressed. Both of these effects amount to a decrease in the entropy of the gas that is not usually compensated by the entropy increase due to mixing of the two kinds of molecules. Such processes greatly restrict the solubility of gases in liquids.
| liquid solvent, solute → | gas |
|---|---|
| energy to disperse solute | nil |
| energy to introduce into solvent | medium to large |
| increase in entropy | negative |
| miscibility | usually very limited |
Solubility of gases in water
Some typical gas solubilities, expressed in the number of moles of gas at 1 atm pressure that will dissolve in a liter of water at 25° C, are given below:
| solute | formula | solubility, mol L–1 atm–1 |
|---|---|---|
| ammonia | NH3 | 57 |
| carbon dioxide | CO2 | 0.0308 |
| methane | CH4 | 0.00129 |
| nitrogen | N2 | 0.000661 |
| oxygen | O2 | 0.00126 |
| sulfur dioxide | SO2 | 1.25 |
As we indicated above, the only gases that are readily soluble in water are those whose polar character allows them to interact strongly with it.
Ammonia is remarkably soluble in water
Inspection of the above table reveals that ammonia is a champion in this regard. At 0° C, one liter of water will dissolve about 90 g (5.3 mol) of ammonia.
NH3 + H2O → NH4+ + OH–
makes no significant contribution to its solubility; the equilibrium lies heavily on the left side (as evidenced by the strong odor of ammonia solutions). Only about four out of every 1000 NH3 molecules are in the form of ammonium ions at equilibrium.
This is truly impressive when one calculates that this quantity of NH3 would occupy (5.3 mol) × (22.4 L mol–1) = 119 L at STP. Thus one volume of water will dissolve over 100 volumes of this gas. It is even more impressive when you realize that in order to compress 119 L of an ideal gas into a volume of 1 L, a pressure of 119 atm would need to be applied! This, together with the observation that dissolution of ammonia is accompanied by the liberation of a considerable amount of heat, tells us that the high solubility of ammonia is due to the formation of more hydrogen bonds (to H2O) than are broken within the water structure in order to accommodate the NH3 molecule.
If we actually compress 90 g of pure NH3 gas to 1 L, it will liquefy, and the vapor pressure of the liquid would be about 9 atm. In other words, the escaping tendency of NH3 molecules from H2O is only about 1/9th of what it is from liquid NH3. One way of interpreting this is that the strong intermolecular (dipole-dipole) attractions between NH3 and the solvent H2O give rise to a force that has the effect of a negative pressure of 9 atm.
The reaction of ammonia with water according to NH3 + H2O → NH4+ + OH–
makes no significant contribution to its solubility; the equilibrium lies heavily on the left side (as evidenced by the strong odor of ammonia solutions) only about four out of every 1000 NH3 molecules are in the form of ammonium ions at equilibrium.
The Ammonia Fountain Experiment
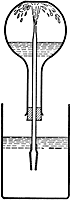This classic experiment nicely illustrates the high solubility of gaseous ammonia in water. A flask fitted with a tube as shown is filled with ammonia gas and inverted so that the open end of tube is submerged in a container of water. A small amount of water is pushed up into the flask to get the process started. As the gas dissolves in the water, its pressure is reduced, creating a partial vacuum that draws additional water into the flask. The effect can be made more dramatic by adding an indicator dye such as phenolphthalein to the water, which turns pink as the water emerges from the "fountain" and becomes alkaline.
"Ammonium hydroxide"
In old textbooks, ammonia's extraordinarily high solubility in water was incorrectly attributed to the formation of the non-existent compound "ammonium hydroxide" NH4OH. Although this formula is still occasionally seen, the name ammonium hydroxide is now used as a synonym for "aqueous ammonia" whose formula is simply NH3(aq).
As can be seen in the table shown previously, the gases CO2 and SO2 also exhibit higher solubilities in water. The main product in each case is a loosely-bound hydrate of the gas, denoted by SO2(aq) or CO2(aq). A very small fraction of the hydrate
CO2·H2O then combines to form carbonic acid H2CO3.
Solubility of gases decreases with temperature
Have you ever noticed the tiny bubbles that form near the bottom of a container of water when it is placed on a hot stove? These bubbles contain air that was previously dissolved in the water, but reaches its solubility limit as the water is warmed. You can completely rid a liquid of any dissolved gases (including unwanted ones such as Cl2 or H2S) by boiling it in an open container.
This is quite different from the behavior of most (but not all) solutions of solid or liquid solutes in liquid solvents. The reason for this behavior is the very large entropy increase that gases undergo when they are released from the confines of a condensed phase (see marginal box at the left).
Solubility of Oxygen in water
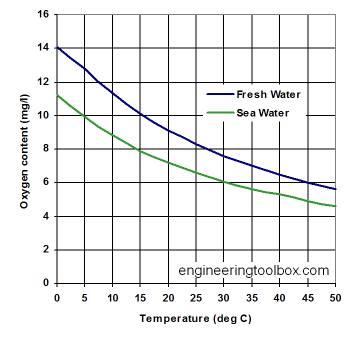Fresh water at sea level dissolves 14.6 mg of oxygen per liter at 0°C and 8.2 mg/L at 25°C. These saturation levels ensure that fish and other gilled aquatic animals are able to extract sufficient oxygen to meet their respiratory needs. But in actual aquatic environments, the presence of decaying organic matter or nitrogenous runoff can reduce these levels far below saturation. The health and survival of these organisms is severely curtailed when oxygen concentrations fall to around 5 mg/L.
The temperature dependence of the solubility of oxygen in water is an important consideration for the well-being of aquatic life; thermal pollution of natural waters (due to the influx of cooling water from power plants) has been known to reduce the dissolved oxygen concentration to levels low enough to kill fish. The advent of summer temperatures in a river can have the same effect if the oxygen concentration has already been partially depleted by reaction with organic pollutants.
The pressure of a gas is a measure of its "escaping tendency" from a phase. So it stands to reason that raising the pressure of a gas in contact with a solvent will cause a larger fraction of it to "escape" into the solvent phase.
The direct-proportionality of gas solubility to pressure was discovered by William Henry (1775-1836) and is known as Henry's Law. It is usually written as
p = kH c
in which p is the partial pressure of the gas above the liquid, c is the concentration of gas dissolved in the liquid, and kH is the Henry's law constant. The latter can be expressed in various units, and in some instances is defined in different ways, so be very careful to note these units when using published values.
In the table below, kH is given as
(partial pressure of gas in atm) ÷ (concentration in liquid, mol L–1)
| gas | He | N2 | O2 | CO2 | CH4 | NH3 |
|---|---|---|---|---|---|---|
| KH | 2703 | 1639 | 769 | 29.4 | .00129 | 57 |
Carbonated beverages: the history of "Fizz-ics"
Artificially carbonated water was first prepared by Joseph Priestley (who later discovered oxygen) in 1767 and was commercialized in 1783 by Joseph Schweppe, a Swiss-German jeweler. Naturally-carbonated spring waters have long been reputed to have curative values, and these became popular tourist destinations in the 19th century. The term "seltzer water" derives from one such spring in Niederselters, Germany.
Of course, carbonation produced by fermentation has been known since ancient times.
The tingling sensation that carbonated beverages produce in the mouth comes from the carbonic acid produced when bubbles of carbon dioxide come into contact with the mucous membranes of the mouth and tongue:
CO2 + H2O → H2CO3.
Some interesting history and facts about carbonated beverages
Solutions of liquids in liquids
Whereas all gases will mix to form solutions regardless of the proportions, liquids are much more fussy. Some liquids, such as ethyl alcohol and water, are miscible in all proportions. Others, like the proverbial oil and water, are not; each liquid has only a limited solubility in the other, and once either of these limits is exceeded, the mixture separates into two phases.
| solute → | liquid |
|---|---|
| energy to disperse solute | varies |
| energy to introduce into solvent | varies |
| increase in entropy | moderate |
| miscibility | "like dissolves like" |
The reason for this variability is apparent from the table. Mixing of two liquids can be exothermic, endothermic, or without thermal effect, depending on the particular substances. Whatever the case, the energy factors are not usually very large, but neither is the increase in randomness; the two factors are frequently sufficiently balanced to produce limited miscibility.
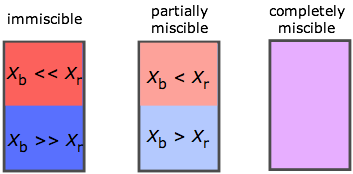
The range of possibilities is shown here in terms of the mole fractions X of two liquids A and B. If A and B are only slightly miscible, they separate into two layers according to their relative densities. Note that when one takes into account trace levels, no two liquids are totally immiscible.
A useful general rule is that liquids are completely miscible when their intermolecular forces are very similar in nature; “like dissolves like”. Thus water is miscible with other liquids that can engage in hydrogen bonding, whereas a hydrocarbon liquid in which London or dispersion forces are the only significant intermolecular effect will only be completely miscible with similar kinds of liquids.
(•-•)Substances such as the alcohols, CH3(CH2)nOH, which are hydrogen-bonding (and thus hydrophilic) at one end and hydrophobic at the other, tend to be at least partially miscible with both kinds of solvents. If n is large, the hydrocarbon properties dominate and the alcohol has only a limited solubility in water. Very small values of n allow the –OH group to dominate, so miscibility in water increases and becomes unlimited in ethanol (n = 1) and methanol (n = 0), but miscibility with hydrocarbons decreases owing to the energy required to break alcohol-alcohol hydrogen bonds when the non polar liquid is added.
These considerations have become quite important in the development of alternative automotive fuels based on mixing these alcohols with gasoline. At ordinary temperatures the increased entropy of the mixture is great enough that the unfavorable energy factor is entirely overcome, and the mixture is completely miscible. At low temperatures, the entropy factor becomes less predominant, and the fuel mixture may separate into two phases, presenting severe problems to the fuel filter and carburetor.
Solutions of molecular solids in liquids
The stronger intermolecular forces in solids require more input of energy in order to disperse the molecular units into a liquid solution, but there is also a considerable increase in entropy that can more than compensate if the intermolecular forces are not too strong, and if the solvent has no strong hydrogen bonds that must be broken in order to introduce the solute into the liquid.
| solvent → | non polar liquid | polar liquid |
|---|---|---|
| energy to disperse solute | moderate | moderate |
| energy to introduce into solvent | small | moderate |
| increase in entropy | moderate | moderate |
| miscibility | moderate | small |
For example, at 25° C and 1 atm pressure, 20 g of iodine crystals will dissolve in 100 ml of ethyl alcohol, but the same quantity of water will dissolve only 0.30 g of iodine.
As the molecular weight of the solid increases, the intermolecular forces holding the solid together also increase, and solubilities tend to fall off; thus the solid linear hydrocarbons CH3(CH2)nCH3 (n > 20) show diminishing solubilities in hydrocarbon liquids.
Solutions of ionic solids in liquids
bic forces that bind ions and highly polar molecules into solids are quite strong, we might expect these solids to be insoluble in just about any solvent. Ionic solids are insoluble in most non-aqueous solvents, but the high solubility of some (including NaCl) in water suggests the need for some further explanation.
| solvent → | non polar | polar (water) |
|---|---|---|
| energy to disperse solute | large | large (endothermic) |
| energy to introduce into liquid | small | highly negative (exothermic) |
| increase in entropy | moderate | moderate to slightly negative |
| miscibility | very small | small to large |
The key factor here turns out to be the interaction of the ions with the solvent. The electrically-charged ions exert a strong coulombic attraction on the end of the water molecule that has the opposite partial charge.
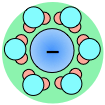
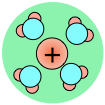As a consequence, ions in solution are always hydrated; that is, they are quite tightly bound to water molecules through ion-dipole interaction. The number of water molecules contained in the primary hydration shell varies with the radius and charge of the ion.
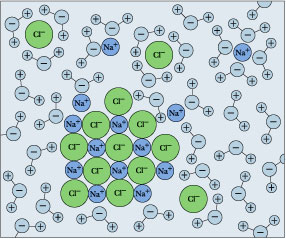
← Hydration shells around some ions in a sodium chloride solution. The average time an ion spends in a shell is about 2-4 nanoseconds. But this is about two orders of magnitude longer than the lifetime of an individual H2O–H2O hydrogen bond.
[U. of Virginia]
Lattice and hydration energies
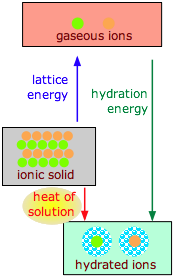
The dissolution of an ionic solid MX in water can be thought of as a sequence of two steps:
(1) MX(s) → M+(g) + X–(g) ΔH >0 (lattice energy)
(2) M+(g) + X–(g) + H2O → M+(aq) + X–(aq) ΔH < 0 (hydration energy)
- The first reaction is always endothermic; it takes a lot of work to break up an ionic crystal lattice.
- The hydration step is always exothermic as H2O molecules are attracted into the electrostatic field of the ion.
- The heat (enthalpy) of solution is the sum of the lattice and hydration energies, and can have either sign.
| H+(g) | –1075 | F–(g) | –503 |
| Li+(g) | –515 | Cl–(g) | –369 |
| Na+(g) | –405 | Br–(g) | –336 |
| K+(g) | –321 | I–(g) | –398 |
| Mg2+(g) | –1922 | OH–(g) | –460 |
| Ca2+(g) | –1592 | NO3– | –328 |
| Sr2+(g) | –1445 | SO42– | –1145 |
| F– | Cl– | Br– | I– | |
| Li+ | +1031 | +848 | +803 | +759 |
| Na+ | +918 | +780 | +742 | +705 |
| K+ | +817 | +711 | +679 | +651 |
| Mg2+ | +2957 | +2526 | +2440 | +2327 |
| Ca2+ | +2630 | +2258 | +2176 | +2074 |
| Sr2+ | +2492 | +2156 | +2075 | +1963 |
Single-ion hydration energies (as shown in the table at upper right) cannot be observed directly, but are obtained from the differences in hydration energies of salts (which are measurable; see below) having the given ion in common.
Additional values can be found on this Wikipedia page and in Chapter 4 of J. Burgess' book Ions in Solution.
Lattice energies are not measured directly, but are estimates based on electrostatic calculations which are reliable only for simple salts. Enthalpies of solution are observable either directly or (for sparingly soluble salts,) indirectly. Hydration energies are not measurable; they are estimated as the sum the other two quantities.
It follows that any uncertainty in the lattice energies is reflected in those of the hydration energies. For this reason, tabulated values of the latter will vary depending on the source.
As often happens for a quantity that is the sum of two large terms having opposite signs, the overall dissolution process can come out as either endothermic or exothermic, and examples of both kinds are common.
substance → |
LiF | NaI | KBr | CsI | LiCl | NaCl | KCl | AgCl |
|---|---|---|---|---|---|---|---|---|
| lattice energy | 1021 | 682 | 669 | 586 | 846 | 778 | 707 | 910 |
| hydration energy | 1017 | 686 | 649 | 552 | 884 | 774 | 690 | 844 |
| enthalpy of solution | +3 | –4 | +20 | +34 | –38 | +4 | +17 | +66 |
Two common examples illustrate the contrast between exothermic and endothermic heats of solution of ionic solids:
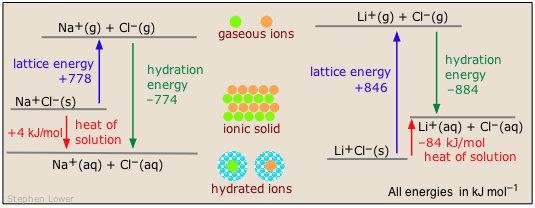
More on heats/enthalpies of solution and hydration at this U. of Waterloo site.
How hydration entropy affects solubility
Hydration shells around some ions in a sodium chloride solution. The average time an ion spends in a shell is about 2-4 nanoseconds. But this is about two orders of magnitude longer than the lifetime of an individual H2O–H2O hydrogen bond.
The balance between the lattice energy and hydration energy is a major factor in determining the solubility of an ionic crystal in water, but there is another factor to consider as well. We generally assume that there is a rather large increase in the entropy when a solid is dispersed into the liquid phase. However, in the case of ionic solids, each ion ends up surrounded by a shell of oriented water molecules. These water molecules, being constrained within the hydration shell, are unable to participate in the spreading of thermal energy throughout the solution, and reduce the entropy. In some cases this effect predominates so that dissolution of the salt leads to a net decrease in entropy. Recall that any process in which the the entropy diminishes becomes less probable as the temperature increases; this explains why the solubilities of some salts decrease with temperature.
