Solutions are homogeneous (single-phase) mixtures of two or more components. For convenience, we often refer to the majority component as the solvent; minority components are solutes. But there is really no fundamental distinction between them.
Solutions play a very important role in Chemistry because they allow intimate and varied encounters between molecules of different kinds, a condition that is essential for rapid chemical reactions to occur. Several more explicit reasons can be cited for devoting a significant amount of effort to the subject of solutions:
- For the reason stated above, most chemical reactions that are carried out in the laboratory and in industry, and that occur in living organisms, take place in solution.
- Solutions are so common; very few pure substances are found in nature.
- Solutions provide a convenient and accurate means of introducing known small amounts of a substance to a reaction system. Advantage is taken of this in the process of titration, for example.
- The physical properties of solutions are sensitively influenced by the balance between the intermolecular forces of like and unlike (solvent and solute) molecules. The physical properties of solutions thus serve as useful experimental probes of these intermolecular forces.
We usually think of a solution as a liquid made by adding a gas, a solid or another liquid solute in a liquid solvent. Actually, solutions can exist as gases and solids as well. Gaseous mixtures don't require any special consideration beyond what you learned about Dalton’s Law earlier in the course.
Solid solutions are very common; most natural minerals and many metallic alloys are solid solutions.
Still, it is liquid solutions that we most frequently encounter and must deal with. Experience has taught us that sugar and salt dissolve readily in water, but that “oil and water don’t mix”. Actually, this is not strictly correct, since all substances have at least a slight tendency to dissolve in each other. This raises two important and related questions: why do solutions tend to form in the first place, and what factors limit their mutual solubilities?
Concentration is a general term that expresses the quantity of solute contained in a given amount of solution. Various ways of expressing concentration are in use; the choice is usually a matter of convenience in a particular application. You should become familiar with all of them.
Parts-per concentration
In the consumer and industrial world, the most common method of expressing the concentration is based on the quantity of solute in a fixed quantity of solution. The “quantities” referred to here can be expressed in weight, in volume, or both (i.e., the weight of solute in a given volume of solution.) In order to distinguish among these possibilities, the abbreviations (w/w), (v/v) and (w/v) are used.
In most applied fields of Chemistry, (w/w) measure is often used, and is commonly expressed as weight-percent concentration, or simply "percent concentration". For example, a solution made by dissolving 10 g of salt with 200 g of water contains "1 part of salt per 20 g of water".
(L. centum), as in century or centennial. It also denotes 1/100th (from L. centesimus) as in centimeter and the monetary unit cent.
It is usually more convenient to express such concentrations as "parts per 100", which we all know as "percent". So the solution described above is a "5% (w/w) solution" of NaCl in water.
In clinical chemistry, (w/v) is commonly used, with weight expressed in grams and volume in mL (see Problem Example 1 below).
Percent means parts per 100; we can also use parts per thousand (ppt) for expressing concentrations in grams of solute per kilogram of solution. For more dilute solutions, parts per million (ppm) and parts per billion (109; ppb) are used. These terms are widely employed to express the amounts of trace pollutants in the environment.
Weight/volume and volume/volume concentrations
It is sometimes convenient to base concentration on a fixed volume, either of the solution itself, or of the solvent alone. In most instances, a 5% by volume solution of a solid will mean 5 g of the solute dissolved in 100 ml of the solvent.
If the solute is itself a liquid, volume/volume measure usually refers to the volume of solute contained in a fixed volume of solution (not solvent). The latter distinction is important because volumes of mixed substances are not strictly additive.
These kinds of concentration measure are mostly used in commercial and industrial applications.
Molarity: mole/volume basis
This is the method most used by chemists to express concentration, and it is the one most important for you to master. Molar concentration (molarity) is the number of moles of solute per liter of solution.
The important point to remember is that the volume of the solution is different from the volume of the solvent; the latter quantity can be found from the molarity only if the densities of both the solution and of the pure solvent are known. Similarly, calculation of the weight-percentage concentration from the molarity requires density information; you are expected to be able to carry out these kinds of calculations, which are covered in most texts.
Normality and equivalents: you can probably forget about them!
Normality is a now-obsolete concentration measure based on the number of equivalents per liter of solution. Although the latter term is now also officially obsolete, it still finds some use in clinical- and environmental chemistry and in electrochemistry. Both terms are widely encountered in pre-1970 textbooks and articles.
The equivalent weight of an acid is its molecular weight divided by the number of titratable hydrogens it carries. Thus for sulfuric acid H2SO4, one mole has a mass of 98 g, but because both hydrogens can be neutralized by strong base, its equivalent weight is 98/2 = 49 g. A solution of 49 g of H2SO4 per liter of water is 0.5 molar, but also "1 normal" (1N = 1 eq/L). Such a solution is "equivalent" to a 1M solution of HCl in the sense that each can be neutralized by 1 mol of strong base.
The concept of equivalents is extended to salts of polyvalent ions; thus a 1M solution of FeCl3 is said to be "3 normal" (3 N) because it dissociates into three moles/L of chloride ions.
Mole fraction: mole/mole basis
This is the most fundamental of all methods of concentration measure, since it makes no assumptions at all about volumes. The mole fraction of substance i in a mixture is defined as
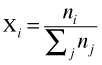 (2-1)
(2-1)
in which nj is the number of moles of substance j, and the summation is over all substances in the solution. Mole fractions run from zero (substance not present) to unity (the pure substance).
The sum of all mole fractions in a solution is, by definition, unity:
![]() (2-2)
(2-2)
In the case of ionic solutions, each kind of ion acts as a separate component.
Calculating solution molality
A 1-molal solution contains one mole of solute per 1 kg of solvent. Molality is a hybrid concentration unit, retaining the convenience of mole measure for the solute, but expressing it in relation to a temperature-independent mass rather than a volume. Molality, like mole fraction, is used in applications dealing with certain physical properties of solutions; we will see some of these in the next lesson.
Conversion between concentration measures
Anyone doing practical chemistry must be able to convert one kind of concentration measure into another. The important point to remember is that any conversion involving molarity requires a knowledge of the density of the solution.
Calculations involving dilution of solutions
These kinds of calculations arise frequently in both laboratory and practical applications. If you have a thorough understanding of concentration definitions, they are easily tackled. The most important things to bear in mind are
- Concentration is inversely proportional to volume;
- Molarity is expressed in mol L–1, so it is usually more convenient to express volumes in liters rather than in mL;
- Use the principles of unit cancellations to determine what to divide by what.


