Avogadro's number and the Mole
Introduction to the mole concept in chemistry
The chemical changes we observe always involve discrete numbers of atoms that rearrange themselves into new configurations. These numbers are HUGE— far too large in magnitude for us to count or even visualize, but they are still numbers, and we need to have a way to deal with them. We also need a bridge between these numbers, which we are unable to measure directly, and the weights of substances, which we do measure and observe. The mole concept provides this bridge, and is central to all of quantitative chemistry.
Owing to their tiny size, atoms and molecules cannot be counted by direct observation. But much as we do when "counting" beans in a jar, we can estimate the number of particles in a sample of an element or compound if we have some idea of the volume occupied by each particle and the volume of the container.
Once this has been done, we know the number of formula units (to use the most general term for any combination of atoms we wish to define) in any arbitrary weight of the substance. The number will of course depend both on the formula of the substance and on the weight of the sample. But if we consider a weight of substance that is the same as its formula (molecular) weight expressed in grams, we have only one number to know: Avogadro's number, 6.022141527 × 1023, usually designated by NA.
Amadeo Avogadro (1766-1856) never knew his own number!
Avogadro only originated the concept of this number, whose actual value was first estimated by Josef Loschmidt, an Austrian chemistry teacher, in 1895.
You should know it to three significant figures:
NA = 6.02 × 1023
6.02 × 1023 of what? Well, of anything you like: apples, stars in the sky, burritos. But the only practical use for NA is to have a more convenient way of expressing the huge numbers of the tiny particles such as atoms or molecules that we deal with in chemistry. Avogadro's number is a collective number, just like a dozen.
Think of 6.02 × 1023 as the "chemist's dozen".
(If the foregoing problems don't make sense, you should review the previous lesson.)
Things to understand about Avogadro's number NA
• It is a number, just as is "dozen", and thus is dimensionless.
• It is a huge number, far greater in magnitude than we can visualize; see here for some interesting comparisons with other huge numbers.
• Its practical use is limited to counting tiny things like atoms, molecules, "formula units", electrons, or photons.
• The value of NA can be known only to the precision that the number of atoms in a measurable weight of a substance can be estimated. Because large numbers of atoms cannot be counted directly, a variety of ingenious indirect measurements have been made involving such things as Brownian motion and X-ray scattering.
• The current value was determined by measuring the distances between the atoms of silicon in an ultrapure crystal of this element that was shaped into a perfect sphere. (The measurement was made by X-ray scattering.) When combined with the measured mass of this sphere, it yields Avogadro's number. But there are two problems with this: 1) The silicon sphere is an artifact, rather than being something that occurs in nature, and thus may not be perfectly reproducible. 2) The standard of mass, the kilogram, is not precisely known, and its value appears to be changing. For these reasons, there are proposals to revise the definitions of both NA and the kilogram. See here for more, and stay tuned!
The mole (abbreviated mol) is the the SI measure of quantity of a "chemical entity", which can be an atom, molecule, formula unit, electron or photon. One mol of anything is just Avogadro's number of that something. Or, if you think like a lawyer, you might prefer the official SI definition:
Avogadro's number NA = 6.02 × 1023, like any pure number, is dimensionless. However, it also defines the mole, so we can also express NA as
6.02 × 1023 mol–1; in this form, it is properly known as Avogadro's constant. This construction emphasizes the role of Avogadro's number as a conversion factor between number of moles and number of "entities".
Molar mass (atomic weight) of a formula unit
The atomic weight, molecular weight, or formula weight of one mole of the fundamental units (atoms, molecules, or groups of atoms that correspond to the formula of a pure substance) is the ratio of its mass to 1/12 the mass of one mole of C12 atoms, and being a ratio, is dimensionless. But at the same time, this molar mass (as many now prefer to call it) is also the observable mass of one mole (NA) of the substance, so we frequently emphasize this by stating it explicitly as so many grams (or kilograms) per mole: g mol–1.
Don't let this confuse you; it is very important always to bear in mind that the mole is a number and not a mass. But each individual particle has a mass of its own, so a mole of any specific substance will always have a mass unique to that substance.
Molar volume of a pure substance
This is the volume occupied by one mole of a pure substance. Molar volume depends on the density of a substance and, like density, varies with temperature owing to thermal expansion, and also with the pressure. For solids and liquids, these variables ordinarily have little practical effect, so the values quoted for 1 atm pressure and 25°C are generally useful over a fairly wide range of conditions. This is definitely not the case with gases, whose molar volumes must be calculated for a specific temperature and pressure.
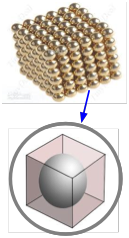
The molar volume of a metallic element allows one to estimate the size of the atom. The idea is to mentally divide a piece of the metal into as many little cubic boxes as there are atoms, and then calculate the length of each box. Assuming that an atom sits in the center of each box and that each atom is in direct contact with its six neighbors (two along each dimension), this gives the diameter of the atom. The manner in which atoms pack together in actual metallic crystals is usually more complicated than this and it varies from metal to metal, so this calculation only provides an approximate value.


