Chemical Formulas and their arithmetic
How to understand and use formulas in calculations
At the heart of chemistry are substances — elements or compounds— which have a definite composition which is expressed by a chemical formula. In this unit you will learn how to write and interpret chemical formulas both in terms of moles and masses, and to go in the reverse direction, in which we use experimental information about the composition of a compound to work out a formula.
This stuff is important! It's not the most interesting part of chemistry, but it is by far the most fundamental in terms of most applications of the subject. Without a thorough understanding of the "chemical arithmetic" in this and the following lesson, you will find yourself stumbling through the remainder of the course.
In order to help you achieve this understanding, this lesson breaks down the subject into much smaller increments than is usually found in textbooks. If you can work through and understand each of the many problem examples presented below, you will be well on your way!
The formula of a compound specifies the number of each kind of atom present in one molecular unit of a compound. Since every unique chemical substance has a definite composition, every such substance must be describable by a chemical formula.
Note that:
- The number of atoms of each element is written as a subscript;
- When only a single atom of an element is present, the subscript is omitted.
- In the case of organic (carbon-containing) compounds, it is customary to place the symbols of the elements C, H, (and if present,) O, N in this order in the formula.
Formulas of elements
The symbol of an element is the one- or two-letter combination that represents the atom of a particular element, such as Au (gold) or O (oxygen). The symbol can be used as an abbreviation for an element name (it is easier to write "Mb" instead of "molybdenum"!) In more formal chemical use, an element symbol can also stand for one atom, or, depending on the context, for one mole (Avogadro's number) of atoms of the element.
Some of the non-metallic elements exist in the form of molecules containing two or more atoms of the element. These molecules are described by formulas such as N2, S6, and P4. Some of these elements can form more than one kind of molecule; the best-known example of this is oxygen, which can exist as O2 (the common form that makes up 21% of the molecules in air), and also as O3, an unstable and highly reactive molecule known as ozone. The soccer-ball-shaped carbon molecules sometimes called buckyballs have the formula C60.
Formulas of ions
Ions are atoms or molecules that carry an electrical charge. These charges are represented as superscripts in the ionic formulas. Thus:
| Cl– | the chloride ion, with one negative charge per atom |
| S2– | the sulfide ion carries two negative charges |
| HCO32– | the hydrogen carbonate ("bicarbonate") ion— a molecular ion |
| NH4+ | the ammonium ion |
Note that the number of charges (in units of the electron charge) should always precede the positive or negative sign, but this number is omitted when the charge is ±1.
Formulas of extended solids and minerals
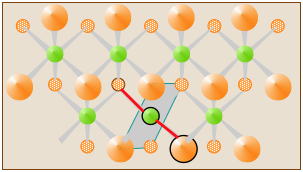
In solid CdCl2, the Cl and Cd atoms are organized into sheets that extend indefinitely. Each atom is surrounded by six atoms of the opposite kind, so one can arbitrarily select any CdCl2 unit as the "molecular unit". One such unit is indicated by the two red-colored bonds in the diagram, but it does not constitute a discrete "molecule" of CdCl2.
Many apparently "simple" solids exist only as ionic solids (such as NaCl) or as extended solids (such as CuCl2) in which no discrete molecules can be identified. The formulas we write for these compounds simply express relative numbers of the different kinds of atoms in the compound in the smallest possible integer numbers. These are identical with the empirical or "simplest" formulas that we discuss further on.
Many minerals and most rocks contain varying ratios of certain elements and can only be precisely characterized at the structural level. Because these are usually not pure substances, the "formulas" conventionally used to describe them have limited meanings.
For example the common rock olivine, which can be considered a solid solution of Mg2SiO4 and Fe2SiO4, can be represented by (Mg,Fe)2SiO4. This implies that the ratio of the metals to SiO4 is constant, and that magnesium is usually present in greater amount than iron.
Empirical of "simplest" formulas
Empirical formulas give the relative numbers of the different elements in a sample of a compound, expressed in the smallest possible integers. The term empirical refers to the fact that formulas of this kind are determined experimentally; such formulas are also commonly referred to as simplest formulas.
Some solid compounds do not exist as discrete molecular units, but are built up as extended two- or three-dimensional lattices of atoms or ions. The compositions of such compounds are commonly described by their simplest formulas. In the very common case of ionic solids, such a formula also expresses the minimum numbers of positive and negative ions required to produce an electrically neutral unit, as in NaCl or CuCl2.
What formulas don’t tell us
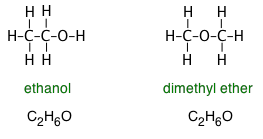
The formulas we ordinarily write convey no information about the compound's structure— that is, the order in which the atoms are connected by chemical bonds or are arranged in three-dimensional space. This limitation is especially significant in organic compounds, in which hundreds if not thousands of different molecules may share the same empirical formula.
The compounds ethanol and dimethyl ether both have the simplest formula C2H6O. The structural formulas reveal the very different nature of these two molecules:
Formulas can be made to convey structural information
It is often useful to write formulas in such as way as to convey at least some information about the structure of a compound. For example, the formula of the solid (NH4)2CO3 is immediately identifiable as ammonium carbonate, and essentially a compound of ammonium and carbonate ions in a 2:1 ratio, whereas the simplest or empirical formula N2H8CO3 obscures this information.
Similarly, the distinction between ethanol and dimethyl ether can be made by writing the formulas as C2H5OH and CH3–O–CH3, respectively. Although neither of these formulas specifies the structures precisely, anyone who has studied organic chemistry can work them out, and will immediately recognize the –OH (hydroxyl) group which is the defining characteristic of the large class of organic compounds known as alcohols. The –O– atom linking two carbons is similarly the defining feature of ethers.
Several related terms are used to express the mass of one mole of a substance.
- Molecular weight This is analogous to atomic weight: it is the relative weight of one formula unit of the compound, based on the carbon-12 scale. The molecular weight is found by adding atomic weights of all the atoms present in the formula unit. Molecular weights, like atomic weights, are dimensionless; i.e., they have no units.
- Formula weight The same thing as molecular weight. This term is sometimes used in connection with ionic solids and other substances in which discrete molecules do not exist.
- Molar mass The mass (in grams, kilograms, or anyother mass unit) of one mole of particles or formula units. When expressed in grams, the molar mass is numerically the same as the molecular weight, but it must be accompanied by the mass unit.
Mole ratios and mole fractions from formulas
The information contained in formulas can be used to compare the compositions of related compounds as in the following example:
Alternatively, one sometimes uses mole fractions to express the same thing. The mole fraction of an element M in a compound is just the number of atoms of M divided by the total number of atoms in the formula unit.
Percent composition and elemental masses from formulas
Since the formula of a compound expresses the ratio of the numbers of its constituent atoms, a formula also conveys information about the relative masses of the elements it contains. But in order to make this connection, we need to know the relative masses of the different elements.
The mass fraction of an element in a compound is just the ratio of the mass of that element to the mass of the entire formula unit. Mass fractions are always between 0 and 1, but are frequently expressed as percent.
Finding the percentage composition of a compound from its formula is a fundamental calculation that you must master; the technique is exactly as shown above. Finding a mass fraction is often the first step in solving related kinds of problems:
Mass ratios of two elements in a compound can be found directly from the mole ratios that are expressed in formulas.
As was explained above, the simplest formula (empirical formula) is one in which the relative numbers of the various elements are expressed in the smallest possible whole numbers. Aluminum chloride, for example, exists in the form of structural units having the composition Al2Cl6; the simplest formula of this substance is AlCl3.
Simplest formulas from atom ratios
Some methods of analysis provide information about the relative numbers of the different kinds of atoms in a compound.
The process of finding the formula of a compound from an analysis of its composition depends on your ability to recognize the decimal equivalents of common integer ratios such as 2:3, 3:2, 4:5, etc.
Simplest formulas from mass composition
More commonly, an arbitrary mass of a compound is found to contain certain masses of its elements. These must be converted to moles in order to find the formula.
Simplest formulas from mass ratios
The composition of a binary (two-element) compound is sometimes expressed as a mass ratio. The easiest approach here is to treat the numbers that express the ratio as masses, thus turning the problem into the kind described immediately above.
Simplest formulas from percent composition
The composition-by-mass of a compound is most commonly expressed as weight percent (grams per 100 grams of compound). The first step is again to convert these to relative numbers of moles of each element in a fixed mass of the compound. Although this fixed mass is completely arbitrary (there is nothing special about 100 grams!), the ratios of the mole amounts of the various elements are not arbitrary: these ratios must be expressible as integers, since they represent ratios of integral numbers of atoms.
Elemental analysis in the laboratory
One of the most fundamental operations in chemistry consists of breaking down a compound into its elements (a process known as analysis) and then determining the simplest formula from the relative amounts of each kind of atom present in the compound. In only a very few cases is it practical to carry out such a process directly: thus heating mercury(II) sulfide results in its direct decomposition: 2 HgS → 2Hg + O2. Similarly, electrolysis of water produces the gases H2 and O2 in a 2:1 volume ratio.
Most elemental analyses must be carried out indirectly, however. The most widely used of these methods has traditionally been the combustion analysis of organic compounds. An unknown hydrocarbon CaHbOc can be characterized by heating it in an oxygen stream so that it is completely decomposed into gaseous CO2 and H2O. These gases are passed through tubes containing substances which absorb each gas selectively. By careful weighing of each tube before and after the combustion process, the values of a and b for carbon and hydrogen, respectively, can be calculated. The subscript c for oxygen is found by subtracting the calculated masses of carbon and hydrogen from that of the original sample.
For analyses of compounds containing elements other than C, H, and O, spectroscopic methods based on atomic absorption and inductively-coupled plasma atomic absorption are now widely used.
The analytical balance
Measurements of mass or weight have long been the principal tool for understanding chemical change in a quantitative way. Balances and weighing scales have been in use for commercial and pharmaceutical purposes since the beginning of recorded history, but these devices lacked the 0.001-g precision required for quantitative chemistry and elemental analysis carried out on the laboratory scale.
It was not until the mid-18th century that the Scottish chemist Joseph Black invented the equal arm analytical balance. The key feature of this invention was a lightweight, rigid beam supported on a knife-edged fulcrum; additional knife-edges supported the weighing pans. The knife-edges greatly reduced the friction that limited the sensitivity of previous designs; it is no coincidence that accurate measurements of combining weights and atomic weights began at about this time.
Analytical balances are enclosed in a glass case to avoid interference from air currents, and the calibrated weights are handled with forceps to prevent adsorption of moisture or oils from bare fingers.
Anyone who was enrolled in college-level general chemistry up through the 1960's will recall the training (and tedium) associated with these devices. These could read directly to 1 milligram and allow estimates to ±0.1 mg. Later technical refinements added magnetic damping of beam swinging, pan brakes, and built-in weight sets operated by knobs. The very best research-grade balances achieved precisions of 0.001 mg.

