The standard cell potentials we discussed in a previous section refer to cells in which all dissolved substances are at unit activity, which essentially means an "effective concentration" of 1M. Similarly, any gases that take part in an electrode reaction are at an effective pressure (known as the fugacity) of 1 atm. If these concentrations or pressures have other values, the cell potential will change in a manner that can be predicted from the principles you already know.
Suppose, for example, that we reduce the concentration of Zn2+ in the Zn/Cu cell from its standard effective value of 1M to an to a much smaller value:
Zn(s) | Zn2+(aq,.001 M) || Cu2+(aq) | Cu(s)
This smaller Zn2+ concentration will reduce the value of Q = [Cu2+] / [ Zn2+] for the cell reaction
Zn(s) + Cu2+ → Zn2+ + Cu(s)(1-1)
thus making it more spontaneous, or "driving it to the right" as the Le Châtelier principle would predict, and making its free energy change ΔG more negative than ΔG°, so that E would be more positive than E°.
The relation between the actual cell potential E and the standard potential E° is developed in the following way. We begin with the equation discussed in the previous lesson which relates the standard free energy change (for the complete conversion of products into reactants) to the standard potential
ΔG° = –nFE° (1-2)
By analogy we can write the more general equation
ΔG = –nFE(1-3)
which expresses the change in free energy for any extent of reaction— that is, for any value of the reaction quotient Q. We now substitute these into the expression that relates ΔG and ΔG° which you will recall from the chapter on chemical equilibrium:
ΔG = ΔG° + RT ln Q(1-4)
which gives
–nFE = –nFE° + RT ln Q(1-5)
which can be rearranged to
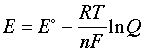 (1-6)
(1-6)
This is the very important Nernst equation which relates the cell potential to the standard potential and to the activities of the electroactive species. Notice that the cell potential will be the same as E° only if Q is unity. The Nernst equation is more commonly written in base-10 log form and for 25°C:
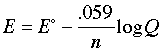
 The Nernst equation tells us that a half-cell potential will change by 59 millivolts per 10-fold change in the concentration of a substance involved in a one-electron oxidation or reduction; for two-electron processes, the variation will be 28 millivolts per decade concentration change.
The Nernst equation tells us that a half-cell potential will change by 59 millivolts per 10-fold change in the concentration of a substance involved in a one-electron oxidation or reduction; for two-electron processes, the variation will be 28 millivolts per decade concentration change.
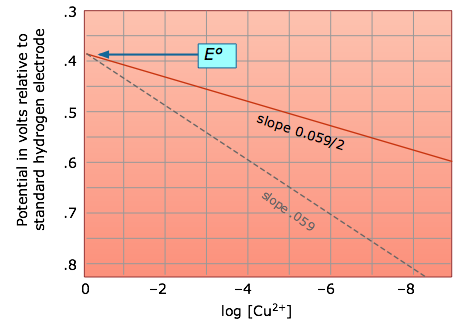
Thus for the dissolution of metallic copper
Cu(s) → Cu2+ + 2e–
the potential
E = (– 0.337) – .0295 log [Cu2+]
becomes more positive (the reaction has a greater tendency to take place) as the cupric ion concentration decreases. This, of course, is exactly what the Le Châtelier Principle predicts; the more dilute the product, the greater the extent of the reaction.
Electrodes without poise
 The equation just above for the Cu/Cu2+ half-cell raises an interesting question: suppose you immerse a piece of copper in a solution of pure water. With
The equation just above for the Cu/Cu2+ half-cell raises an interesting question: suppose you immerse a piece of copper in a solution of pure water. With
Q = 1 / [Cu2+] = 1 / 0, the potential difference between the electrode and the solution should be infinite! Are you in danger of being electrocuted? You need not worry; without any electron transfer, there is no charge to zap you with. Of course it won't be very long before some Cu2+ ions appear in the solution, and if there are only a few such ions per liter, the potential reduces to only about 20 volts, More to the point, however, the system is so far from equilibrium (for example, there are not enough ions to populate the electric double layer that normally surrounds electrodes,) that the Nernst equation doesn't really give meaningful results. Such an electrode is said to be unpoised.
What ionic concentration is needed to poise an electrode? I don't really know, but I would be suspicious of anything much below 10–6 M.
The Nernst equation works only in dilute solutions
Ions of opposite charge tend to associate into loosely-bound ion pairs in more concentrated solutions, thus reducing the number of ions that are free to donate or accept electrons at an electrode. For this reason, the Nernst equation cannot accurately predict half-cell potentials for solutions in which the total ionic concentration exceeds about 103 M.
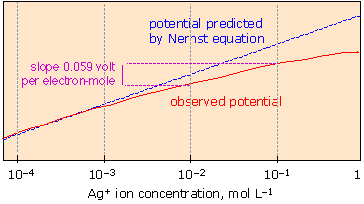
How the cell potential really depends on concentration!
The Nernst equation accurately predicts cell potentials only when the equilibrium quotient term Q is expressed in activities. Ionic activities depart increasingly from concentrations when the latter exceed 10–4 to 10–5 M, depending on the sizes and charges of the ions. |
 |
Activities and activity coefficients
If the Nernst equation is applied to more concentrated solutions, the terms in the reaction quotient Q must be expressed in "effective concentrations" or activities of the electroactive ionic species. The activity coefficient γ (gamma) relates the concentration of an ion to its activity a in a given solution through the relation a = γc. Since electrode potentials measure activities directly, activity coefficients can be determined by carrying out appropriate EMF measurements on cells in which the concentration of the ion of interest is known. The resulting E's can then be used to convert concentrations into activities for use in other calculations involving equilibrium constants.
As most of us recall from our struggles with balancing redox equations in beginning chemistry courses, many electron-transfer reactions involve hydrogen ions and hydroxide ions. The standard potentials for these reactions therefore refer to the pH, either 0 or 14, at which the appropriate ion has unit activity. Because multiple numbers of H+ or OH– ions are often involved, the potentials given by the Nernst equation can vary greatly with the pH.
It is frequently useful to look at the situation in another way by considering what combinations of potential and pH allow the stable existence of a particular species. This information is most usefully expressed by means of a E-vs.-pH diagram, also known as a stability- or Pourbaix diagram.
The utility of these diagrams is illustrated by the following three examples that are of considerable practical importance.
Stability diagram of water
As was noted in connection with the shaded region in the figure below, water is subject to decomposition by strong oxidizing agents such as Cl2 and by reducing agents stronger than H2. The reduction reaction can be written either as
2H+ + 2e– → H2(g)(3-1)
or, in neutral or alkaline solutions as
H2O + 2 e– → H2(g) + 2 OH–(3-2)
These two reactions are equivalent and follow the same Nernst equation
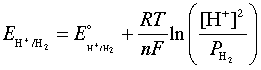 (3-3)
(3-3)
which, at 25°C and unit H2 partial pressure reduces to
E = E° - (.059/2) × 2 pH = –0.059 pH(3-4)
Similarly, the oxidation of water
2 H2O → O2(g) + 4 H+ + 4 e–(3-5)
is governed by the Nernst equation
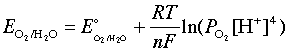 (3-6)
(3-6)
which, under the same stanard conditions, becomes
E = 1.23 – 0.059 pH(3-7)
Notice that (3-4) and (3-7) are equations of a straight line whose slopes are identical, indicating that the potentials become more negative as the pH increases. Plotting these E-values as functions of the pH yields the Pourbaix diagram for water which clearly shows its range of stability.
Stability diagrams are able to condense a great amount of information into a compact representation, and are widely employed in geochemistry and corrosion engineering.
Stability of chlorine in water
Because chlorine is widely used as a disinfectant for drinking water, swimming pools, and sewage treatment, it is worth looking at its stability diagram. Note that the effective bactericidal agent is not Cl2 itself, but its oxidation product hypochlorous acid HOCl which predominates at pH values below its pKa of 7.3.
Pourbaix diagram for iron
As the final example, we will consider the very important Pourbaix diagram for iron, which is of considerable interest to those concerned with protecting it from corrosion.
From your study of thermodynamics you may recall that the process
solute (concentrated) → solute (dilute)
is accompanied by a fall in free energy, and therefore is capable of doing work on the surroundings; all that is required is some practical way of capturing this work. One way of doing this is by means of a concentration cell such as the this one which represents the transport of cupric ion from a region of higher concentration to one of lower concentration:
Cu(s) | CuNO3(.01 M) || CuNO3(.1 M) | Cu(s)
| reduction: | Cu2+(.1 M) + 2e– → Cu(s) |
| oxidation: | Cu(s)→ Cu2+(.01 M) + 2e– |
| net: | Cu2+(.1 M)→ Cu2+(.01 M) |
The driving force for this process is the free energy change ΔG associated with the concentration gradient (C2 – C1), sometimes known as the free energy of dilution:
ΔGdilution = RT ln(C2 – C1)
The Nernst equation for this cell is
E = E° - (0.059/N) log Q = 0 - 0.29 log 0.1 = +0.285 v
Note that E° for a concentration cell is always zero, since this would be the potential of a cell in which the electroactive species are at unit activity in both compartments.
An interesting aspect of this kind of cell is that Cu2+ ions need not physically move between the two compartments; electron flow through the external circuit creates a "virtual" flow as copper ions are created in the low-concentration side and discharged at the opposite electrode. However, in order to maintain electroneutraliy, there must be a pathway between the two solutions that allows nitrate ions must also pass between the half cells.

