Differential and integral rate laws

Measuring instantaneous rates as we have described on the previous page of this unit is the most direct way of determining the rate law of a reaction, but is not always convenient, and it may not even be possible to do so with any precision.

• If the reaction is very fast, its rate may change more rapidly than the time required to measure it; the reaction may be finished before even an initial rate can be observed.
• In the case of very slow reactions, observable changes in concentratons occur so slowly that the observation of a truly "instantaneous" rate becomes impractical.

The ordinary rate law (more precisely known as the instantaneous or differential rate law) tells us how the rate of a reaction depends on the concentrations of the reactants. But for many practical purposes, it is more important to know how the concentrations of reactants (and of products) change with time.

For example, if you are carrying out a reaction on an industrial scale, you would want to know how long it will take for, say, 95% of the reactants to be converted into products.

This is the purpose of an integrated rate law.

Expressing the "speed" of a reaction: the half-life

How long does it take for a chemical reaction to occur under a given set of conditions? As with many "simple" questions, no meaningful answer can be given without being more precise. In this case,

How do we define the point at which the reaction is "completed"?

A reaction is "completed" when it has reached equilibrium — that is, when concentrations of the reactants and products are no longer changing.

If the equilibrium constant is quite large, then the answer reduces to a simpler form: the reaction is completed when the concentration of a reactant falls to zero. In the interest of simplicity, we will assume that this is the case in the remainder of this discussion.

"How long?" may be too long

If the reaction takes place very slowly, the time it takes for every last reactant molecule to disappear may be too long for the answer to be practical. In this case, it might make more sense to define "completed" when a reactant concentration has fallen to some arbitrary fraction of its initial value — 90%, 70%, or even only 20%.

The particular fraction one selects depends on the cost of the reactants in relation to the value of the products, balanced against the cost of operating the process for a longer time or the inconvenience of waiting for more product. This kind of consideration is especially imporant in industrial processes in which the balances of these costs affect the profitability of the operation.

The half-life of a reaction

Instead of trying to identify the time required for the reaction to become completed, it is far more practical to specify the the time required for the concentration of a reactant to fall to half of its initial value. This is known as the half-life (or half-time) of the reaction.

First-order reactions

The law of exponential change

The rate at which a reactant is consumed in a first-order process is proportional to its concentration at that time. This general relationship, in which a quantity changes at a rate that depends on its instantaneous value, is said to follow an exponential law.

The first-order integrated rate law

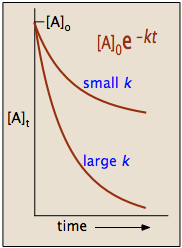The integrated rate law for a first-order reaction

A → products

is a common example of the law of exponential change. For a reactant A, its concentration [A]_t at time t is given by

[A]_t = [A]_o × e^–kt

in which [A]_o is its initial concentration and k is the first-order rate constant.

The "e" in the exponential term is of course the base of the natural logarithms, and the negative sign in its exponent means that the value of this term diminishes as t increases, as we would expect for any kind of a decay process.

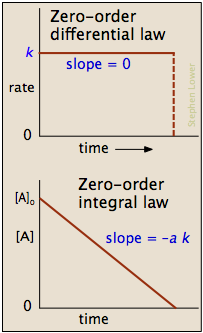
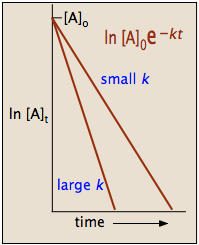A more convenient form of the integrated rate law is obtained by taking the natural logarithm of both sides:

ln [A] = –kt + ln [A]_o(4-1)

This has the form of an equation for a straight line

y = mx + b

in which the slope m corresponds to the rate constant k. This means that, for a first-order reaction, a plot of ln [A] as a function of time gives a straight line with a slope of –k.

Half-life

After a period of one half-life, t = t_½ and we can write

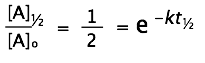
(in which we express the exponential as a function in order to make it stand out more prominently.) Taking logarithms of both sides (remember that
ln e^x = x) yields

Solving for the half-life, we obtain the simple relation

which tells us that the half-life of a first-order reaction is a constant. This means that 100,000 molecules of a reactant will be reduced to 50,000 in the same time interval needed for ten molcules to be reduced to five.

 

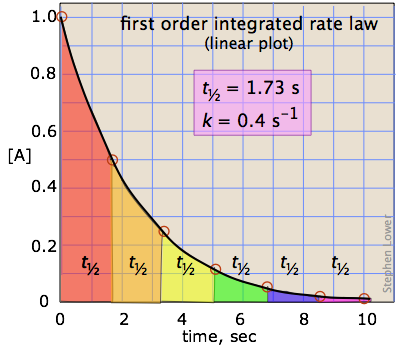
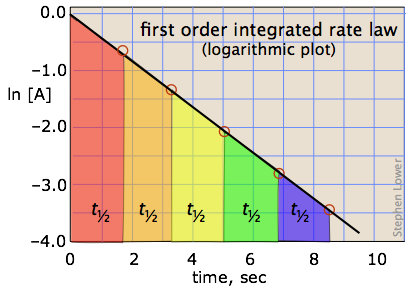
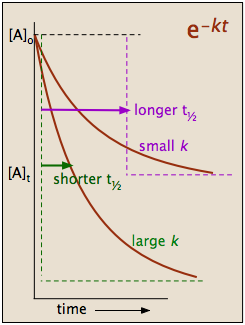
It should be clear that the rate constant and the half life of a first-order process are inversely related.

The decay of radioactive nuclei is always a first-order process.

Second-order reactions

Integration of the second-order rate law

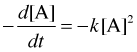
yields

which is easily rearranged into a form of the equation for a straight line (try showing this yourself!) and yields plots similar to the one shown on the left below.

The half-life is given by

(see here for details)

Notice that the half-life of a second-order reaction depends on the initial concentration, in contrast to its constancy for a first-order reaction. For this reason, the concept of half-life for a second-order reaction is far less useful.

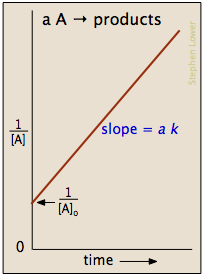
Zero-order processes

In some reactions, the rate is apparently independent of the reactant concentraton, in which case

rate = k [A]⁰ = k

Note the word "apparently" in the preceding sentence; zero-order kinetics is always an artifact of the conditions under which the reaction is carried out. For this reason, reactions that follow zero-order kinetics are often referred to as pseudo-zero-order reactions.

Clearly, a zero-order process cannot continue after a reactant has been exhausted. Just before this point is reached, the reaction will revert to another rate law instead of falling directly to zero as depicted at the upper left.

There are two general conditions that can give rise to zero-order rates:

1. Only a small fraction of the reactant molecules are in a location or state in which they are able to react, and this fraction is continually replenished from the larger pool.

This situation commonly occurs when a reaction is catalyzed by attachment to a solid surface (heterogeneous catalysis) or to an enzyme.

For example, the decomposition of nitrous oxide

N₂O → N₂(g) + ½ O₂(g)

in the presence of a hot platinum wire (which acts as a catalyst) is zero-order, but it follows more conventional kinetics when carried out entirely in the gas phase.

In this case, the N₂O molecules that react are limited to those that have attached themselves to the surface of the solid catalyst. Once all of the sites on the limited surface of the catalyst have been occupied, additional gas-phase molecules must wait until the decomposition of one of the adsorbed molecules frees up a surface site.

Enzyme-catalyzed reactions in organisms begin with the attachment of the substrate to the active site on the enzyme, leading to the formation of an enzyme-substrate complex. If the number of enzyme molecules is limited in relation to substrate molecules, then the reaction may appear to be zero-order.

2. When two or more reactants are involved, the concentrations of some are much greater than those of others

This is most often seen when two or more reactants are involved. Thus if the reaction

 A + B → products

is first-order in both reactants so that

rate = k [A][B]

then if B is present in great excess, the reaction will appear to be zero order in B (and first order overall). This commonly happens when B is H₂O and the reaction is carried out in aqueous solution.

 

The following table compares the rate parameters of zero-, first-, and second-order reactions of the form aA → products. See also this excellent page from Purdue University that shows plots of [A], ln [A], and 1/[A] for each reaction order.

	zero order	first order	second order
differential rate law	rate = k	rate = k[A]	rate = k[A]2
integrated rate law	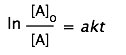[A] = [A]ο = –akt
half-life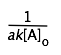
plot that gives straight line	[A] vs. t	ln [A] vs. t	1/[A] vs. t
plot, showing interpretation of slope and intercept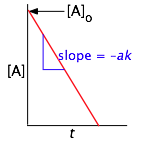

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially imortant that you know the precise meanings of all the green-highlighted terms in the context of this topic.

• Describe the contrasting roles of thermodynamics and kinetics in understanding chemical change.
• Given a balanced net equation, write an expression for the rate of a reaction.
• Sketch a curve showing how the instantaneous rate of a reaction might change with time.
• Determine the order of a reaction of the form  A → B + C  from experimental data for the concentrations of its products at successive times.
• Describe the initial rate and isolation methods of determining the orders of the individual reactants in a reaction involving multiple reactants.
• Explain the difference between differential and integral rate laws.
• Sketch out a plot showing how the concentration of a component ([A] or ln [A]) that follows first-order kinetics will change with time. Indicate how the magnitude of the rate constant affects this plot
• Define the half-life of a reaction.
• Given the half-life for a first-order reaction  A → products  along with the initial value of [A]_o, find [A]_t at a subsequent time an integral number of half-lifes later.
• Describe the conditions under which a reaction can appear to have an order of zero.