Measuring instantaneous rates as we have described above is the most direct way of determining the rate law of a reaction, but is not always convenient, and it may not even be possible to do so with any precision.
- If the reaction is very fast, its rate may change more rapidly than the time required to measure it; the reaction may be finished before even an initial rate can be observed.
- In the case of very slow reactions, observable changes in concentratons occur so slowly that the idea of a truly "instantaneous" rate loses its meaning.
The rate law tells us how the rate of a reaction depends on the concentrations of the reactants. But for many practical purposes, it is more important to know how the concentrations of reactants (and of products) change with time.
For example, if you are carrying out a reaction on an industrial scale, you would want to know how long it will take for, say, 95% of the reactants to be converted into products.
This is the purpose of an integrated rate law.
Integrating the first-order rate law
In the terms of calculus, the rate laws we have been discussing are essentially derivatives of concentrations
d[A]/dt = –k [A] (i)
and they can thus be integrated with respect to time to give the concentration of a component after a given interval. Integrating the above expression is denoted by
∫d[A] = -k ∫[A] dt (ii)
or
which, by the rules of calculus, gives
ln [A] = –kt + C (iii)
To evaluate the integration constant C, let [A]o be the concentration of the reactant at time 0. This yields
C = ln [A]o (v)
so that integrated rate law is
ln [A] = –kt + ln [A]o (i)
which we rearrange to
Solving for [A] at time t, we obtain the exponential form of the integrated rate law
[A]t = [A]o e–kt
The integrated rate law
ln [A] = –kt + ln [A]o(4-1)
has the form of an equation for a straight line
y = mx + b
in which the slope m corresponds to the rate constant k. This means that, for a first-order reaction, a plot of ln [A] as a function of time gives a straight line with a slope of –k.
The half-life of a first-order reaction
The half-life of a reaction is the time required for the concentration of a reactant to decrease to half of its initial value. It is the single most useful parameter for describing the speed of a reaction. Additionally, it provides a convenient way of determining the reaction order.
If the initial concentration of a reactant is [A]o, then after one half-life t½ has passed, [A] = ½[A]o.
Making this substitution into the integrated rate law, we obtain
ln ½[A]o = –kt½ + ln [A]o (4-2)
Combining the [A]o terms gives the simple result
ln ( [A]o / 0.5[A]o ) = ln 2 = 0.693 (4-3)
so the half-life becomes
t½ = 0.693 / k (4-4) Important!
which shows that the half-life of a first-order reactant is independent of its concentration — an extremely useful and important relationship.
Integrating the second-order rate law
To integrate the second-order instantaneous rate law
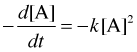
we first rearrange it to
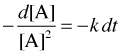
Integration yields
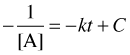
To evaluate the integration constant, let [A]o = [A] at time t = 0, so that
After one half-life, [A] = ½[A]o
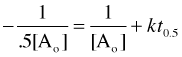
or
The important thing to notice here is that the half-life depends on the initial concentration.
Pseudounimolecular reactions
A bimolecular reaction step always follows a second-order rate law
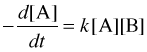
The Chem1 Virtual Textbook home page is at http://www.chem1.com/acad/virtualtextbook.html

This work is licensed under a
Creative Commons Attribution-Share Alike 3.0 License.
