General Chemistry Virtual Textbook → dynamics 1 → rates and rate laws
Rates of reactions
and rate laws
On this page:
Chemical change is guided and driven by energetics, but the actual route it takes and the speed with which it occurs is the subject of "dynamics". Dynamics is itself divided into two general areas: kinetics, which deals with the rate of change and is the subject of this lesson. Mechanistics, introduced in a later lesson, is an exploration of the "road map" that links reactants to products.
The energetic aspects of change are governed by the laws of thermodynamics (the "dynamics" part of this word is related to the historical origins of the field and is not a part of dynamics in the sense of these lessons.)
Thermodynamics points the way and makes it possible
Chemical change is driven by the tendency of atoms and molecules to rearrange themselves in a way that results in the maximum possible dispersion of thermal energy into the world. The observable quantity that measures this spreading and sharing of energy is the free energy of the system. As a chemical change takes place, the quantities of reactants and products change in a way that leads to a more negative free energy. When the free energy reaches its minimum possible value, there is no more net change and the system is said to be in equilibrium.
The beauty of thermodynamics is that it enables us to unfailingly predict the net direction of a reaction and the composition of the equilibrium state even without conducting the experiment; the standard free energies of the reactants and products, which can be independently measured or obtained from tables, are all we need.
...but it says nothing about how long it will take to get there!
The "speed" of a reaction — how long it takes to reach equilibrium — bears no relation at all to how spontaneous it is (as given by the sign and value of ΔG°) or whether it is exothermic or endothermic (given by the sign of ΔH°). Moreover, there is no way that reaction rates can be predicted in advance; each reaction must be studied individually. One reason for this is that
the stoichiometric equation for the reaction says nothing about its mechanism
By mechanism, we mean, basically, "who does what to whom". Think of a reaction mechanism as something that goes on in a "black box" that joins reactants to products:

The inner workings of the black box are ordinarily hidden from us, are highly unpredictable and can only be inferred by indirect means. Consider, for example, the gas-phase formation reactions of the hydrogen halides from the elements.
Three reactions that look alike, but are not
The thermodynamics of these reactions are all similar (they are all highly exothermic), but their dynamics (their kinetics and mechanisms) could not be more different.
Careful experiments, carried out over many years, are consistent with the simplest imaginable mechanism: a collision between the two reactant molecules results in a rearrangement of the bonds:
|
One might be tempted to suppose that this would proceed in a similar way, . but experiments reveal that the mechanism of this reaction is far more complex. The reaction takes place in a succession of steps, some of which involve atomic H and Br. |
The mechanism of this reaction is different again. Although the first two reactions reach equilibrium in minutes to an hour or so at temperatures of 300 to 600 K, a mixture of hydrogen and chlorine will not react at all in the dark, but if you shine a light on the mixture, it goes off with a bang as the instantaneous reaction releases heat and expands the gas explosively. |
... and what is particularly noteworthy is that these striking differences cannot be reliably predicted from theory; they were revealed only by experimentation.
Chemical reactions vary greatly in the speed at which they occur. Some are essentially instantaneous, while others may take years to reach equilibrium.
Definition of reaction rate
The speed of a chemical reaction may be defined as the change in concentration of a substance divided by the time interval during which this change is observed:
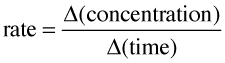 (2-1) important definition !
(2-1) important definition !
For a reaction of the form A + B → C, the rate can be expressed in terms of the change in concentration of any of its components:
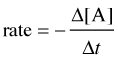 |
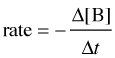 |
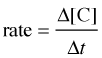 |
in which Δ[A] is the difference between the concentration of A over the time interval t2 – t1:
Δ[A] = [A]2 – [A]1 (2-2)
Notice the minus signs in the equations shown in the two leftmost boxes above.
The concentration of a reactant always decreases with time, so Δ[A] and Δ[B] are both negative. Since negative rates don't make much sense, rates expressed in terms of a reactant concentration are always preceded by a minus sign in order to make the rate come out positive.
Consider now a reaction in which the coefficients are different:
A + 3B → 2D
It is clear that [B] decreases three times as rapidly as [A], so in order to avoid ambiguity when expressing the rate in terms of different components, it is customary to divide each change in concentration by the appropriate coefficient:
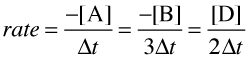 (2-3)
(2-3)
So please understand: each of the above quotients is a legitimate expression of the rate of this particular reaction; they all yield the same number. Which one you employ when doing a calculation is largely a matter of convenience.
For the oxidation of ammonia 4 NH3 + 3O2 = 2 N2 + 6 H2O
it was found that the rate of formation of N2 was 0.27 mol L–1 s–1.
a) At what rate was water being formed?
b) At what rate was ammonia being consumed?
Solution:
a) From the equation stoichiometry, Δ[H2O] = 6/2 Δ[N2], so the rate of formation of H2O is 3 × (0.27 mol L–1 s–1) = 0.81 mol L–1 s–1.
b) 4 moles of NH3 are consumed for every 2 moles of N2 formed, so the rate of disappearance of ammonia is 2 × (0.27 mol L–1 s–1) = 0.54 mol L–1 s–1.
Comment: Because of the way this question is formulated, it would be acceptable to express this last value as a negative number.
Instantaneous rates
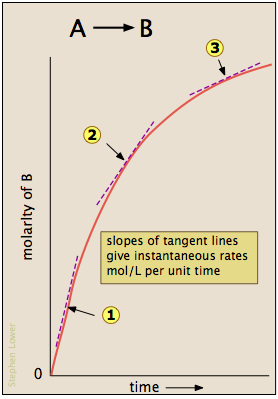 Most reactions slow down as the reactants are consumed. Consequently, the rates given by the expressions shown above tend to lose their meaning when measured over longer time intervals Δt.
Most reactions slow down as the reactants are consumed. Consequently, the rates given by the expressions shown above tend to lose their meaning when measured over longer time intervals Δt.
Note: Instantaneous rates are also known as differential rates.
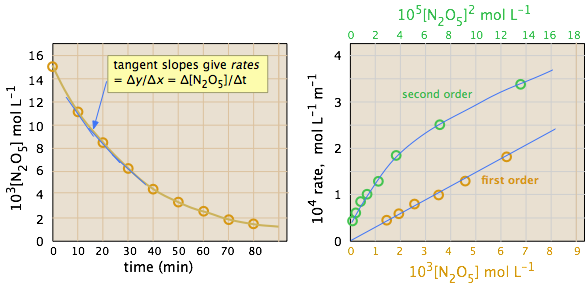
Thus for the reaction whose progress is plotted here, the actual rate (as measured by the increasing concentration of product) varies continuously, being greatest at time zero. The instantaneous rate of a reaction is given by the slope of a tangent to the concentration-vs.-time curve. Three such rates have been identified in this plot.
An instantaneous rate taken near the beginning of the reaction (t = 0) is known as an initial rate (label (1) here). As we shall soon see, initial rates play an important role in the study of reaction kinetics.
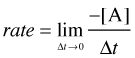
... but if you don't know calculus, just bear in mind that the larger the time interval Δt, the smaller will be the precision of the instantaneous rate.
The relation between the rate of a reaction and the concentrations of reactants is expressed by its rate law. For example, the rate of the gas-phase decomposition of dinitrogen pentoxide
2N2O5 → 4NO2 + O2
has been found to be directly proportional to the concentration of N2O5:
rate = k [N2O5]
Be very careful about confusing equilbrium constant expressions with those for rate laws. The expression for Keq can always be written by inspecting the reaction equation, and it contains a term for each component (raised to the appropriate power) whose concentration changes during the reaction. For this reaction it is given by
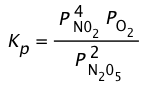
In contrast, the expression for the rate law generally bears no necessary relation to the reaction equation, and must be determined experimentally.
More generally, for a reaction of the form
nA A + nB B + ... → products
the rate law will be
![]()
in which the exponents a and b are usually (but not always) integers (including zero) and, we must emphasize once again, bear no relation to the coefficients nA , nB in the reaction equation.
Since the rate of a reaction has the dimensions of (concentration/time), the dimensions of the rate constant k will depend on the exponents of the concentration terms in the rate law. To make this work out properly, if we let p be the sum of the exponents of the concentration terms in the rate law
p = a + b + ...
then k will have the dimensions (concentration1–p/time).
Reaction order
The order of a rate law is the sum of the exponents in its concentration terms. For the N2O5 decomposition with the rate law k[N2O5], this exponent is 1 (and thus is not explicitly shown); this reaction is therefore a first order reaction. We can also say that the reaction is "first order in N2O5".
For more complicated rate laws, we can speak of the overall reaction order and also the orders with respect to each component. As an example, consider a reaction
A + 3B + 2C → products
whose experimental rate law is
rate = k[A] [B]2
We would describe this reaction as third-order overall, first-order in A, second-order in B, and zero-order in C.
Zero-order means that the rate is independent of the concentration of a particular reactant. But of course enough C must be present to allow the equilibrium mixture to form.
The rate of oxidation of bromide ions by bromate in an acidic aqueous solution
6H+ + BrO3– + 5Br– → 3 Br2 + 3 H2O
is found to follow the rate law
rate = k[Br–][BrO3–][H+]2
What happens to the rate if, in separate experiments, (a) [BrO3–] is doubled; (b) the pH is increased by one unit; (c) the solution is diluted to twice its volume, with the pH kept constant by use of a buffer?
Solution:
(a) Since the rate is first-order in bromate, doubling its concentration will double the reaction rate.
(b) Increasing the pH by one unit will decrease the [H+] by a factor of 10. Since the reaction is second-order in [H+], this will decrease the rate by a factor of 100.
(c) Dilution reduces the concentrations of both Br2 and BrO3– to half their original values. Doing this to each concentration alone would reduce the rate by a factor of 2, so reducing both concentration will reduce the rate by a factor of 4, to (½)×(½) = ¼ of its initial value.
How reaction orders are observed
Observing rate-vs.-concentration proportionality
In order to determine the value of the exponent in a rate equation term, we need to see how the rate varies with the concentration of the substance. For a single-reactant decomposition reaction of the form
A → products
in which the rate is –d[A]/dt, we simply plot [A] as function of time, draw tangents at various intervals, and see how the slopes of these tangents (the instantaneous rates) depend on [A].
- If doubling the concentration of A doubles the rate, then the reaction is first-order in A.
- If doubling the concentration results in a four-fold rate increase, the reaction is second-order in A.
Problem Example 3
Use the tabulated experimental data to determine the order of the reaction
2 N2O5 → 4 NO2 + O2
| Time (min) | p(N2O5) | [N2O5] mol L-1 | Rate mol L-1 min-1 |
|---|---|---|---|
| 0 | 301.6 | 0.0152 | |
| 10 | 224.8 | 0.0113 | 3.4 × 10–4 |
| 20 | 166.7 | 0.0084 | 2.5 |
| 30 | 123.2 | 0.0062 | 1.8 |
| 40 | 92.2 | 0.0046 | 1.3 |
| 69.1 | 69.1 | 0.0035 | 1.0 |
Solution:
The ideal gas law can be used to convert the partial pressures of N2O5 to molar concentrations. These are then plotted (left) to follow their decrease with time. The rates are computed from the slopes of the tangents (blue lines) and their values plotted as a function of [N2O5] and [N2O5]2. It is apparent that the rates are directly proportional to [N2O5]1, indicating that this is a first-order reaction.
Initial rate method
When there is more than one reactant, the method described above is rarely practical, since the concentrations of the different reactants will generally fall at different rates, depending on the stoichiometry. Instead, we measure only the rate near the beginning of the reaction, before the concentrations have had time to change significantly. The experiment is then repeated with a different starting concentration of the reactant in question, but keeping the concentrations of any others the same. After the order with respect to one component is found, another series of trials is conducted in which the order of another component is found.
| Using the same dinitrogen pentoxide decomposition as in the previous example, we conduct a series of runs using five different initial concentrations of N2O5. Note that we use only the tangents at the beginning of each plot — that is, at times t=0. | 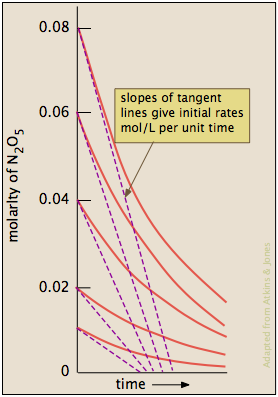
|
| We then plot the five initial rates of consumption of N2O5 as a function of its molar concentration. As before, we see that these rates are directly proportional to [N2O5]. The slope of this plot gives the value of the rate constant. |
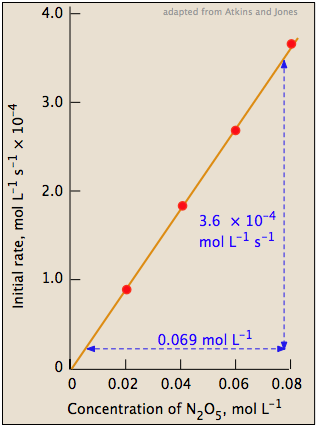 |
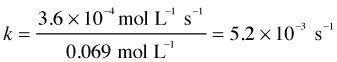
rate = (5.2 × 10–3) [N2O5] mol L–1 s–1
A study of the gas-phase reduction of nitric oxide by hydrogen
2 NO + 2 H2 → N2 + 2 H2O
yielded the following initial-rate data (all pressures in torr):
| experiment | P(NO) | P(H2) | initial rate |
|---|---|---|---|
| 359 | 300 | 1.50 | |
| 300 | 300 | 1.03 | |
| 152 | 300 | 0.25 | |
| 300 | 289 | 1.00 | |
| 300 | 205 | 0.71 | |
| 200 | 147 | 0.51 |
Find the order of the reaction with respect to each component.
In looking over this data, take note of the following:
- The six runs recorded here fall into two groups, in which the initial pressures of H2 and of NO, respectively, are held constant.
- All the data are expressed in pressures, rather than in concentrations. We can do this because the reactants are gases, whose concentrations are directly proportional to their partial pressures when T and V are held constant. And since we are only interested in comparing the ratios of pressures and rates, the units cancel out and don't matter. It is far easier experimentally to adjust and measure pressures than concentratons.
Solution:
Experiments 2 and 3: Reduction of the initial partial pressure of NO by a factor of about 2 (300/152) results in a reduction of the initial rate by a factor of about 4, so the reaction is second-order in nitric oxide.
Experiments 4 and 6: Reducing the initial partial pressure of hydrogen by a factor of approximately 2 (289/147) causes a similar reduction in the initial rate, so the reaction is first-order in hydrogen.
The rate law is thus rate = k[NO]2[H2].
Dealing with multiple reactants: the isolation method
It is not always practical to determine orders of two or more reactants by the method illustrated in the preceding example. Fortunately, there is another way to accomplish the same task: we can use excess concentrations of all the reactants except the one we wish to investigate. For example, suppose the reaction is
A + B + C → products
and we need to find the order with respect to [B] in the rate law. If we set
[B]o to 0.020