About ten years after Bohr had developed his theory, de Broglie showed that the electron should have wavelike properties of its own, thus making the analogy with the mechanical theory of standing waves somewhat less artificial. One serious difficulty with the Bohr model still remained, however: it was unable to explain the spectrum of any atom more complicated than hydrogen. A refinement suggested by Sommerfeld assumed that some of the orbits are elliptical instead of circular, and invoked a second quantum number,
ℓ, that indicated the degree of ellipticity. This concept proved useful, and it also began to offer some correlation with the placement of the elements in the periodic table.
The Schrödinger equation
By 1926, de Broglie's theory of the wave nature of the electron had been experimentally confirmed, and the stage was set for its extension to all matter. At about the same time, three apparently very different theories that attempted to treat matter in general terms were developed. These were Schrödinger's wave mechanics, Heisenberg's matrix mechanics, and a more abstract theory of P.A.M. Dirac. These eventually were seen to be mathematically equivalent, and all continue to be useful.

Of these alternative treatments, the one developed by Schrödinger is the most easily visualized. Schrödinger started with the simple requirement that the total energy of the electron is the sum of its kinetic and potential energies:
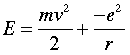
The second term represents the potential energy of an electron (whose charge is denoted by e) at a distance r from a proton (the nucleus of the hydrogen atom). In quantum mechanics it is generally easier to deal with equations that use momentum (p = mv) rather than velocity, so the next step is to make this substitution:
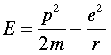
This is still an entirely classical relation, as valid for the waves on a guitar string as for those of the electron in a hydrogen atom. The third step is the big one: in order to take into account the wavelike character of the hydrogen atom, a mathematical expression that describes the position and momentum of the electron at all points in space is applied to both sides of the equation. The function, denoted by Ψ (psi), "modulates" the equation of motion of the electron so as to reflect the fact that the electron manifests itself with greater probability in some locations that at others. This yields the celebrated Schrödinger equation:
If this equation looks a bit weird to you, don't be too concerned; we show it here only because one hears so much about it — quite justifiably, as it "drives" every atom in the universe.
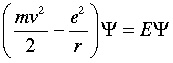
Physical significance of the wave function Ψ
How can such a simple-looking expression contain within it the quantum-mechanical description of an electron in an atom— and thus, by extension, of all matter? The catch, as you may well suspect, lies in discovering the correct form of Ψ , which is known as the wave function. As this nams suggests, the value of Ψ is a function of location in space relative to that of the proton which is the source of the binding force acting on the electron. As in any system composed of standing waves, certain boundary conditions must be applied, and these are also contained in Ψ; the major ones are that the value of Ψ must approach zero as the distance from the nucleus approaches infinity, and that the function be continuous.
When the functional form of Ψ has been worked out, the Schrödinger equation is said to have been solved for a particular atomic system. The details of how this is done are beyond the scope of this course, but the consequences of doing so are extremely important to us. Once the form of is known, the allowed energies E of an atom can be predicted from the above equation. Soon after Schrödinger's proposal, his equation was solved for several atoms, and in each case the predicted energy levels agreed exactly with the observed spectra.
There is another very useful kind of information contained in Ψ. Recalling that its value depends on the location in space with respect to the nucleus of the atom, the square of this function Ψ2, evaluated at any given point in space, represents the probability of finding the electron at that particular location. The significance of this cannot be overemphasized; although the electron remains a particle having a definite charge and mass, the question of "where" it is located is no longer meaningful.
Any single experimental observation will reveal a definite location for the electron, but this will in itself have little significance; only a large number of such observations (similar to a series of multiple exposures of a photographic film) will yield meaningful results which will show that the electron can "be" anywhere with at least some degree of probability. This does not mean that the electron is "moving around" to all of these places, but that (in accord with the uncertainty principle) the concept of location has limited meaning for a particle as small as the electron. If we count only those locations in space at which the probability of the electron manifesting itself exceeds some arbitrary value, we find that the Ψ function defines a definite three-dimensional region which we call an orbital.
Why doesn't the electron fall into the nucleus?
We can now return to the question which Bohr was unable to answer in 1912. Even the subsequent discovery of the wavelike nature of the electron and the analogy with standing waves in mechanical systems did not really answer the question; the electron is still a particle having a negative charge and is attracted to the nucleus.
The answer comes from the Heisenberg uncertainty principle, which says that a quantum particle such as the electron cannot simultaneously have sharply-defined values of location and of momentum (and thus kinetic energy). To understand the implications of this restriction, suppose that we place the electron in a small box. The walls of the box define the precision δx to which the location is known; the smaller the box, the more exactly will we know the location of the electron. But as the box gets smaller, the uncertainty in the electron's kinetic energy will increase. As a consequence of this uncertainty, the electron will at times possess so much kinetic energy (the "confinement energy") that it may be able to penetrate the wall and escape the confines of the box.
This process is known as quantum tunneling. It is exploited in various kinds of semiconductor devices, and it is the mechanism whereby electrons jump between dissolved ions and the electrode in batteries and other electrochemical devices.
(For more, see this Wikipedia article on quantum tunneling)
The region near the nucleus can be thought of as an extremely small funnel-shaped box, the walls of which correspond to the electrostatic attraction that must be overcome if an electron confined within this region is to escape. As an electron is drawn toward the nucleus by electrostatic attraction, the volume to which it is confined diminishes rapidly. Because its location is now more precisely known, its kinetic energy must become more uncertain; the electron's kinetic energy rises more rapidly than its potential energy falls, so that it gets ejected back into one of its allowed values of n.
The electron well of the atom
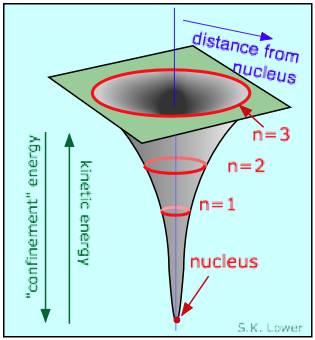
n=1 through n=3. As n decreases, the potential energy of the system becomes more negative and the electron becomes more confined in space. According to the uncertainty principle, this increases the momentum of the electron, and hence its kinetic energy. The latter acts as a kind of "confinement energy" that restores the electron to one of the allowed levels.
The values of n in the above diagram correspond to the principal quantum number of the hydrogen atom. When the H atom is in its normal "ground state", n = 1 and the radius of this circle corresponds exactly to the radius predicted by Bohr's model. The big difference between Bohr's model and the quantum model is that in the latter, the n=1 circle defines the radius at which the electron is most likely to be found, rather than the radius to which it is confined as Bohr's theory predicts.
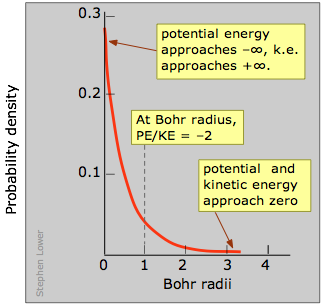
But it doesn't quite make it; as the electron approaches the tiny volume of space occupied by the nucleus, its potential energy dives down toward minus-infinity, and its kinetic energy (momentum and velocity) shoots up toward positive-infinity. This "battle of the infinities" cannot be won by either side, so a compromise is reached in which theory tells us that the fall in potential energy is just twice the kinetic energy, and the electron dances at an average distance that corresponds to the Bohr radius.
Orbits give way to orbitals and electron clouds

The modern view of atomic structure dismisses entirely the old but comfortable planetary view of electrons circling around the nucleus in fixed orbits.
We can also dispose of the question of why the orbiting electron does not radiate its kinetic energy away as it revolves around the nucleus. The Schrödinger equation completely discards any concept of a definite path or trajectory of a particle; what was formerly known as an "orbit" is now an "orbital", defined as the locations in space at which the probability of finding electrons exceeds some arbitrary value. It should be noted that this wavelike character of the electron coexists with its possession of a momentum, and thus of an effective velocity, even though its motion does not imply the existence of a definite path or trajectory that we associate with a more massive particle.
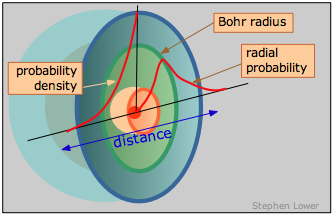
Modern quantum theory tells us that the various allowed states of existence of the electron in the hydrogen atom correspond to different standing wave patterns. In the preceding lesson we showed examples of standing waves that occur on a vibrating guitar string. The wave patterns of electrons in an atom are different in two important ways:
- Instead of indicating displacement of a point on a vibrating string, the electron waves represent the probability that an electron will manifest itself (appear to be located) at any particular point in space. (Note carefully that this is not the same as saying that "the electron is smeared out in space"; at any given instant in time, it is either at a given point or it is not.)
- The electron waves occupy all three dimensions of space, whereas guitar strings vibrate in only two dimensions.
Aside from this, the similarities are striking. Each wave pattern is identified by an integer number n, which in the case of the atom is known as the principal quantum number. The value of n tells how many peaks of amplitude (antinodes) exist in that particular standing wave pattern; the more peaks there are, the higher the energy of the state.
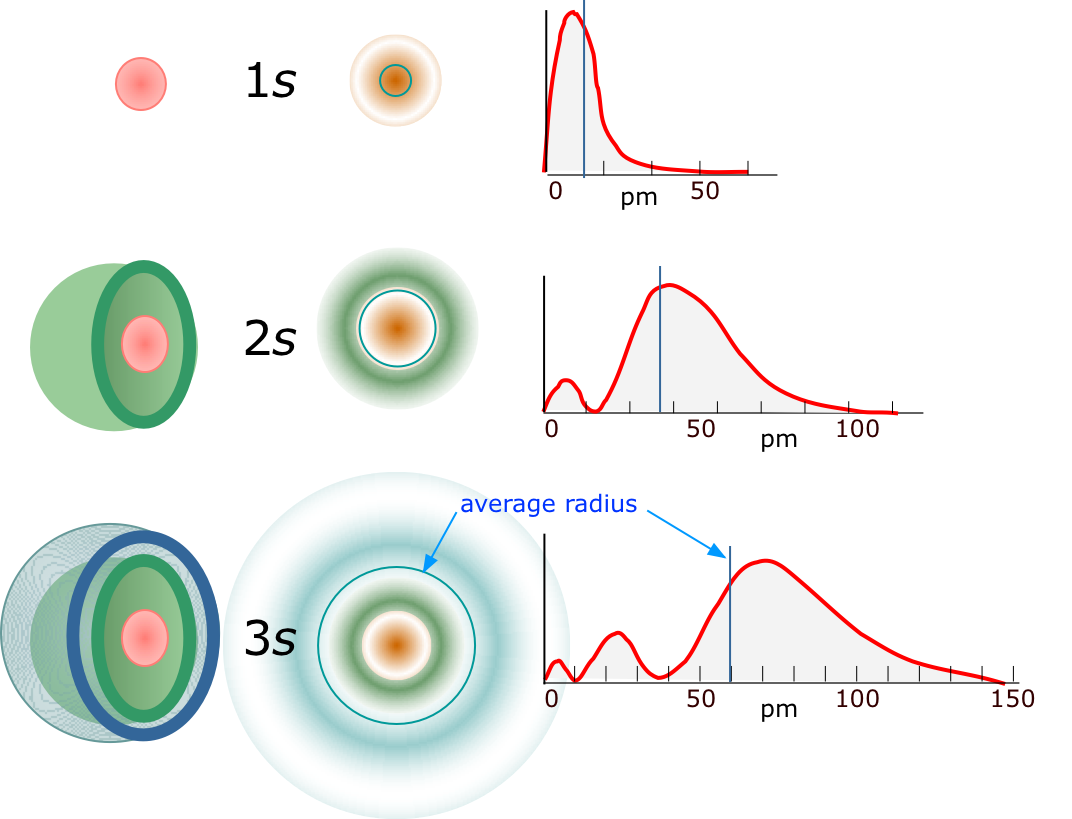
The three simplest orbitals of the hydrogen atom are depicted above in pseudo-3D, in cross-section, and as plots of probability (of finding the electron) as a function of distance from the nucleus. The average radius of the electron probability is shown by the blue circles or plots in the two columns on the right. These radii correspond exactly to those predicted by the Bohr model.
Physical significance of n
The potential energy of the electron is given by the formula
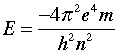
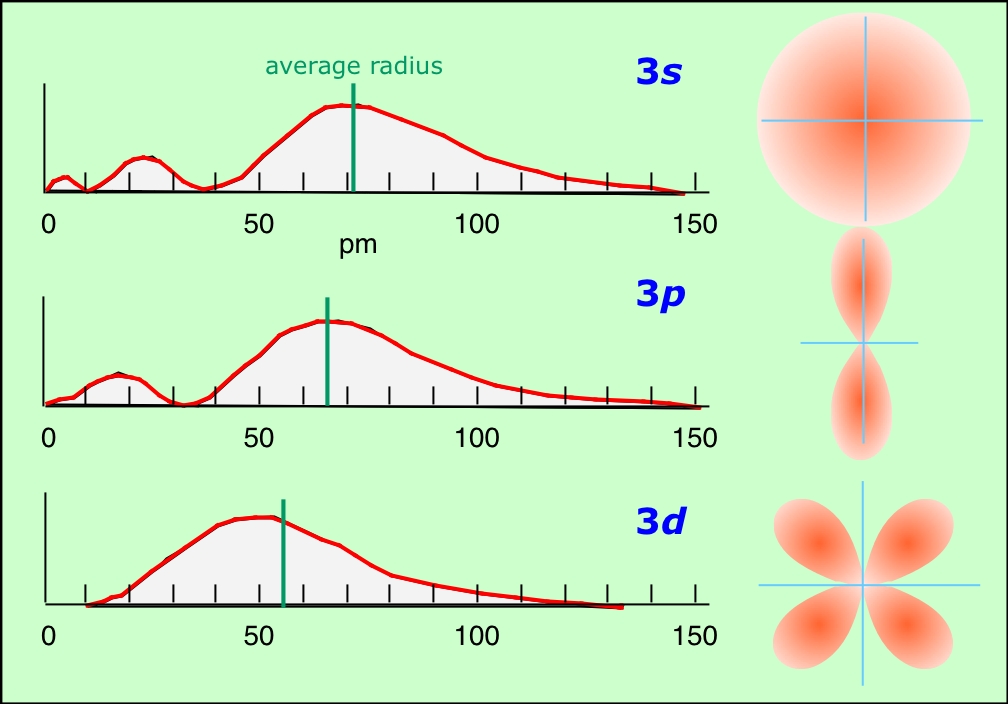
in which e is the charge of the electron, m is its mass, h is Planck's constant, and n is the principal quantum number. The negative sign ensures that the potential energy is always negative. Notice that this energy in inversely proportional to the square of n, so that the energy rises toward zero as n becomes very large, but it can never exceed zero.
This formula was actually part of Bohr's original theory, and is still applicable to the hydrogen atom, although not to atoms containing two or more electrons. In the Bohr model, each value of n corresponded to an orbit of a different radius. The larger the orbital radius, the higher the potential energy of the electron; the inverse square relationship between electrostatic potential energy and distance is reflected in the inverse square relation between the energy and n in the above formula.
Although the concept of a definite trajectory or "orbit" of the electron is no longer tenable, the same orbital radii that relate to the different values of n in Bohr's theory now have a new significance: they give the average distance of the electron from the nucleus. As you can see from the figure, the averaging process must encompass several probability peaks in the case of higher values of n. The spatial distribution of these probability maxima defines the particular orbital.
The angular momentum quantum number
The electron wave functions that are derived from Schrödinger's theory are characterized by several quantum numbers. The first one, n, describes the nodal behavior of the probability distribution of the electron, and correlates with its potential energy and average distance from the nucleus as we have just described.
The angular momentum quantum number is conventionally represented by lower-case L: l. In order to avoid confusion with the numeral 1, it is ordinarily italized:
l. Additional clarity, which we employ here, is provided by using the scripted form: ℓ.
The theory also predicts that orbitals having the same value of n can differ in shape and in their orientation in space. The quantum number ℓ, known as the angular momentum quantum number, determines the shape of the orbital. (More precisely, ℓ determines the number of angular nodes, that is, the number of regions of zero probability encountered in a 360° rotation around the center.)
If ℓ = 1, the orbital is elongated into something resembling a figure-8 shape, and higher values of ℓ correspond to still more complicated shapes— but note that the number of peaks in the radial probability distributions (below) decreases with increasing ℓ. The possible values that ℓ can take are strictly limited by the value of the principal quantum number; ℓ can be no greater than n – 1. This means that for
n = 1, ℓ can only have the single value zero which corresponds to a spherical orbital. For historical reasons, the orbitals corresponding to different values of ℓ are designated by letters, starting with s for ℓ = 0, p for ℓ = 1, d for ℓ = 2, and f for ℓ = 3.
The shapes and radial distributions of the orbitals corresponding to the three allowed values of ℓ for the n = 3 level of hydrogen are shown above. Notice that the average orbital radius r decreases somewhat at higher values of ℓ. The function relationship is given by
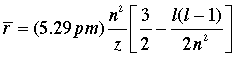
in which z is the nuclear charge of the atom, which of course is unity for hydrogen.
The magnetic quantum number
An s-orbital, corresponding to ℓ = 0, is spherical in shape and therefore has no special directional properties. The probability cloud of a p orbital is aligned principally along an axis extending along any of the three directions of space. The additional quantum number m is required to specify the particular direction along which the orbital is aligned.
"Direction in space" has no meaning in the absence of a force field that serves to establish a reference direction. For an isolated atom there is no such external field, and for this reason there is no distinction between the orbitals having different values of m. If the atom is placed in an external magnetic or electrostatic field, a coordinate system is established, and the orbitals having different values of m will split into slightly different energy levels. This effect was first seen in the case of a magnetic field, and this is the origin of the term magnetic quantum number.
In chemistry, however, electrostatic fields are much more important for defining directions at the atomic level because it is through such fields that nearby atoms in a molecule interact with each other. The electrostatic field created when other atoms or ions come close to an atom can cause the energies of orbitals having different direction properties to split up into different energy levels; this is the origin of the colors seen in many inorganic salts of transition elements, such as the blue color of copper sulfate.
The quantum number m can assume 2ℓ + 1 values for each value of ℓ, from –ℓ through 0 to +ℓ. When ℓ = 0 the only possible value of m will also be zero, and for the p orbital (ℓ = 1), m can be –1, 0, and +1. Higher values of ℓ introduce more complicated orbital shapes which give rise to more possible orientations in space, and thus to more values of m.
Electron spin and the exclusion principle
Certain fundamental particles have associated with them a magnetic moment that can align itself in either of two directions with respect to an external magnetic field. The electron is one such particle, and the direction of its magnetic moment is called its spin.
The mechanical analogy implied by the term spin is easy to visualize, but should not be taken literally. Physical rotation of an electron is meaningless. However, the coordinates of the electron's wave function can be rotated mathematically; when this is done, it is found that a rotation of 720° is required to restore the function to its initial value— rather weird, considering that a 360° rotation will leave any extended body unchanged! Electron spin is basically a relativistic effect in which the electron's momentum distorts local space and time. It has no classical counterpart and thus cannot be visualized other than through mathematics.
A basic principle of modern physics states that for particles such as electrons that possess half-integral values of spin, no two of them can be in identical quantum states within the same system. The quantum state of a particle is defined by the values of its quantum numbers, so what this means is that no two electrons in the same atom can have the same set of quantum numbers. This is known as the Pauli exclusion principle, named after the German physicist Wolfgang Pauli (1900-1958, Nobel Prize 1945).
The best non-mathematical explanation of the exclusion principle that I have come across is Phil Fraundorf's Candle Dances and Atoms page at U. Missouri-St. Louis.
The exclusion principle was discovered empirically and was placed on a firm theoretical foundation by Pauli in 1925. A complete explanation requires some familiarity with quantum mechanics, so all we will say here is that if two electrons possess the same quantum numbers n, l, m and s (defined below), the wave function that describes the state of existence of the two electrons together becomes zero, which means that this is an "impossible" situation.
A given orbital is characterized by a fixed set of the quantum numbers n, ℓ, and m. The electron spin itself constitutes a fourth quantum number s, which can take the two values +1 and –1. Thus a given orbital can contain two electrons having opposite spins, which "cancel out" to produce zero magnetic moment. Two such electrons in a single orbital are often referred to as an electron pair.
More on the Pauli exclusion principle from answers.com
As we have seen, the lowest-energy standing wave pattern the electron can assume in an atom corresponds to n=1, which describes the state of the single electron in hydrogen, and of the two electrons in helium. Since the quantum numbers m and ℓ are zero for n=1, the pair of electrons in the helium orbital have the values (n, l, m, s) = (1,0,0,+1) and (1,0,0,–1)— that is, they differ only in spin. These two sets of quantum numbers are the only ones that are possible for a n=1 orbital. The additional electrons in atoms beyond helium must go into higher-energy (n>1) orbitals.
Electron wave patterns corresponding to these greater values of n are concentrated farther from the nucleus, with the result that these electrons are less tightly bound to the atom and are more accessible to interaction with the electrons of neighboring atoms, thus influencing their chemical behavior. If it were not for the Pauli principle, all the electrons of every element would be in the lowest-energy n=1 state, and the differences in the chemical behavior the different elements would be minimal. Chemistry would certainly be a simpler subject, but it would not be very interesting!