Electron-tunneling model of chemical bonding Chemical bonding occurs when one or more electrons can be simultaneously close to two nuclei. But how can this be arranged? The conventional picture of the shared electron bond places the bonding electrons in the region between the two nuclei. This makes a nice picture, but it is not consistent with the principle you probably learned in Grade 9, that opposite charges attract. This would imply that the electrons would be "happiest" (at the lowest potential energy) when they are very close to a nucleus, not half a bond-length away from two of them!
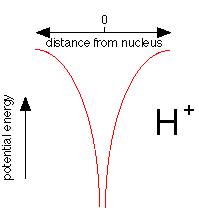
This plot shows how the potential energy of an electron in the hydrogen atom varies with its distance from the nucleus. Notice how the energy falls without limit as the electron approaches the nucleus, represented here as a proton, H+. If potential energy were the only consideration, the electron would fall right into the nucleus where its potential energy would be minus infinity.
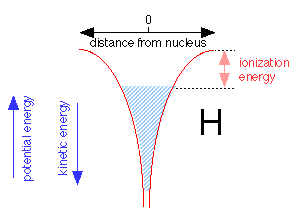When an electron is added to the proton to make a neutral hydrogen atom, it tries to get as close to the nucleus as possible. The Heisenberg Indeterminancy ("uncertainty") principle requires the total energy of the electron energy to increase as the volume of space it occupies diminishes. As the electron gets closer to the nucleus, the nuclear charge confines the electron to such a tiny volume of space that its energy rises, allowing it to "float" slightly away from the nucleus without ever falling into it.
The shaded region above shows the range of energies and distances from the nucleus the electron is able to assume within the 1s orbital. The electron can thus be regarded as a fluid that occupies a vessel whose walls conform to the red potential energy curves shown above. Note that as the potential energy falls, the kinetic energy increases, but only half as fast (this is called the virial theorem.) Thus close to the nucleus, the kinetic energy is large and so is the electron's effective velocity. The top of the shaded area defines the work required to raise its potential energy to zero, thus removing it from the atom; this corresponds, of course, to the ionization energy.
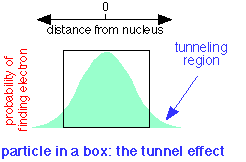A quantum particle can be described by a waveform which is the plot of a mathematical function related to the probability of finding the particle at a given location at any time. If the particle is confined to a box, it turns out that the wave does not fall to zero at the walls of the box, but has a finite probability of being found outside it. This means that a quantum particle is able to penetrate, or "tunnel through" its confining boundaries. This remarkable property is called the tunnel effect.
In terms of the electron fluid model introduced above, the fluid is able to "leak out" of the atom if another low-energy location can be found nearby.
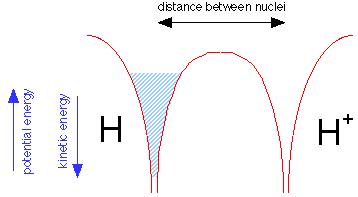Suppose we now bring a bare proton up close to a hydrogen atom. Each nucleus has its own potential well, but only that of the hydrogen atom is filled, as indicated by the shading in the leftmost potential well.
But the electron fluid is able to tunnel through the potential energy barrier separating the two wells; like any liquid, it will seek a common level in the two sides of the container as shown below. The electron is now "simultaneously cose to two nuclei" while never being in between them. Bear in mind that this would be physically impossible for a real liquid composed of real molecules; this is purely a quantum effect that is restricted to a low-mass particle such as the electron.
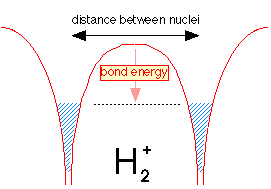
Because the same amount of electron fluid is now shared between the two wells, its level in both is lower. The difference between what it is now and what is was before corresponds to the bond energy of the hydrogen molecule ion.
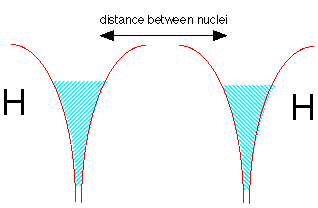
Now let's make a molecule of dihydrogen. We start with two hydrogen atoms, each with one electron. But there is a problem here: both potential energy wells are already filled with electron fluid; there is no room for any more without pushing the energy way up. But quantum theory again comes to the rescue! If the two electrons have opposite spins, the two fluids are able to interpenetrate each other, very much as two gases are able to occupy the same container. This is depicted by the double shading in the diagram below.
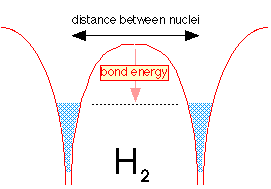
When the two hydrogen atoms are within tunneling distance, half of the electron fluid (really the probabability of finding the electron) from each well flows into the other well. Because the two fluids are able to interpenetrate, the level is not much different from what it was in the H2+ ion, but the greater density of the electron-fluid between the two nuclei makes H2 a strongly bound molecule.
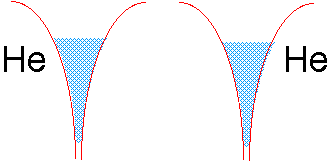
If we tried to join two helium atoms in this way, we would be in trouble. The electron well of He already contains two electrons of opposite spin. There is no room for more electron fluid (without raising the energy), and thus no way the electrons in either He atom can be simultaneously close to two nuclei.
The preceding material was derived from an article by S. Nordholm, J. Chem. Ed. 65(7) 581-584 1988: Delocalization the key concept of covalent bonding.
All errors, omissions and misinterpretations are my own.
(For teachers) Frank Rioux: The Covalent Bond Examined Using the Virial Theorem (Chemical Educator 2003 1)
For a thorough discussion of chemical bonding, see the Chem1 Chemical Bonding Reference Text
© 2003 by Stephen Lower; last updated 2007.02.27
For information about this Web site or to contact the author,
please see the Chem1 Virtual Textbook home page.
This work is licensed under a Creative Commons Attribution-NonCommercial 2.5 License.