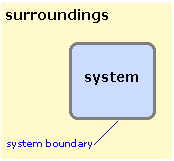
 In thermodynamics, we must be very precise in our use of certain words. The two most important of these are system and surroundings. A thermodynamic system is that part of the world to which we are directing our attention. Everything that is not a part of the system constitutes the surroundings. The system and surroundings are separated by a boundary. If our system is one mole of a gas in a container, then the boundary is simply the inner wall of the container itself. The boundary need not be a physical barrier; for example, if our system is a factory or a forest, then the boundary can be wherever we wish to define it. We can even focus our attention on the dissolved ions in an aqueous solution of a salt, leaving the water molecules as part of the surroundings. The single property that the boundary must have is that it be clearly defined, so we can unambiguously say whether a given part of the world is in our system or in the surroundings.
In thermodynamics, we must be very precise in our use of certain words. The two most important of these are system and surroundings. A thermodynamic system is that part of the world to which we are directing our attention. Everything that is not a part of the system constitutes the surroundings. The system and surroundings are separated by a boundary. If our system is one mole of a gas in a container, then the boundary is simply the inner wall of the container itself. The boundary need not be a physical barrier; for example, if our system is a factory or a forest, then the boundary can be wherever we wish to define it. We can even focus our attention on the dissolved ions in an aqueous solution of a salt, leaving the water molecules as part of the surroundings. The single property that the boundary must have is that it be clearly defined, so we can unambiguously say whether a given part of the world is in our system or in the surroundings.
If matter is not able to pass across the boundary, then the system is said to be closed; otherwise, it is open. A closed system may still exchange energy with the surroundings unless the system is an isolated one, in which case neither matter nor energy can pass across the boundary. The tea in a closed Thermos bottle approximates a closed system over a short time interval.
Properties and the state of a system
The properties of a system are those quantities such as the pressure, volume, temperature, and its composition, which are in principle measurable and capable of assuming definite values. There are of course many properties other than those mentioned above; the density and thermal conductivity are two examples. However, the pressure, volume, and temperature have special significance because they determine the values of all the other properties; they are therefore known as state properties because if their values are known then the system is in a definite state.
Change of state: the meaning of Δ
In dealing with thermodynamics, we must be able to unambiguously define the change in the state of a system when it undergoes some process. This is done by specifying changes in the values of the different state properties using the symbol Δ (delta) as illustrated here for a change in the volume:
ΔV = Vfinal – Vinitial(1-1)
We can compute similar delta-values for changes in P, V, ni (the number of moles of component i), and the other state properties we will meet later.
Internal energy is simply the totality of all forms of kinetic and potential energy of the system. Thermodynamics makes no distinction between these two forms of energy and it does not assume the existence of atoms and molecules. But since we are studying thermodynamics in the context of chemistry, we can allow ourselves to depart from “pure” thermodynamics enough to point out that the internal energy is the sum of the kinetic energy of motion of the molecules, and the potential energy represented by the chemical bonds between the atoms and any other intermolecular forces that may be operative.
How can we know how much internal energy a system possesses? The answer is that we cannot, at least not on an absolute basis; all scales of energy are arbitrary. The best we can do is measure changes in energy. However, we are perfectly free to define zero energy as the energy of the system in some arbitrary reference state, and then say that the internal energy of the system in any other state is the difference between the energies of the system in these two different states.
The First Law
This law is one of the most fundamental principles of the physical world. Also known as the Law of Conservation of Energy, it states that energy can not be created or destroyed; it can only be redistributed or changed from one form to another.
A way of expressing this law that is generally more useful in Chemistry is that any change in the internal energy of a system is given by the sum of the heat q that flows across its boundaries and the work w done on the system by the surroundings.
important ⇒ΔU = q + w (2-1)must know this!
This says that there are two kinds of processes, heat and work, that can lead to a change in the internal energy of a system. Since both heat and work can be measured and quantified, this is the same as saying that any change in the energy of a system must result in a corresponding change in the energy of the world outside the system- in other words, energy cannot be created or destroyed.
The full significance of Eq. 1 cannot be grasped without understanding that U is a state function. This means that a given change in internal energy ΔU can follow an infinite variety of pathways corresponding to all the possible combinations of q and w that can add up to a given value of ΔU.
As a simple example of how this principle can simplify our understanding of change, consider two identical containers of water initially at the same temperature. We place a flame under one until its temperature has risen by 1°C. The water in the other container is stirred vigorously until its temperature has increased by the same amount. There is now no physical test by which you could determine which sample of water was warmed by performing work on it, by allowing heat to flow into it, or by some combination of the two processes. In other words, there is no basis for saying that one sample of water now contains more “work”, and the other more “heat”. The only thing we can know for certain is that both samples have undergone identical increases in internal energy, and we can determine the value of simply by measuring the increase in the temperature of the water.
There seems to be no end of schemes perpetrated by cranks, kooks (and perhaps even a few crooks!) to foist off onto the science-naïve public, crackpot schemes to obtain "free energy" from various sources, usually in blissful ignorance of the First Law. Schemes for using water as a fuel are especially popular, as can be seen on the many Web sites promoting devices that electrolytically decompose water to create H2/O2 mixtures that are given exotic names such as "Aquafuel" and "Brown's Gas" or "HHO" .) These hucksters fail to mention that somebody has to pay for the electricity used to operate these goofy devices!
The kind of work most frequently associated with chemical change occurs when the volume of the system changes owing to the disappearance or formation of gaseous substances. This is sometimes called expansion work or PV-work, and it can most easily be understood by reference to the simplest form of matter we can deal with, the hypothetical ideal gas.
The figure shows a quantity of gas confined in a cylinder by means of a moveable piston. Weights placed on top of the piston exert a force f over the cross-section area A, producing a pressure P = f / A which is exactly countered by the pressure of the gas, so that the piston remains stationary. Now suppose that we heat the gas slightly; according to Charles’ law, this will cause the gas to expand, so the piston will be forced upward by a distance
Δx. Since this motion is opposed by the force f, a quantity of work f Δx will be done by the gas on the piston. By convention, work done by the system (in this case, the gas) on the surroundings is negative, so the work is given by
w = – f Δx(3-1)
When dealing with a gas, it is convenient to think in terms of the more relevant quantities pressure and volume rather than force and distance. We can accomplish this by multiplying the second term by A/A which of course leaves it unchanged:
![]() (3-2)
(3-2)
By grouping the terms differently, but still not changing anything, we obtain
![]() (3-3)
(3-3)
Since pressure is force per unit area and the product of the length A and the area has the dimensions of volume, this expression becomes
w = –P ΔV (3-4)
It is important to note that although P and V are state functions, the work is not (that's why we denote it by a lower-case w.) As is shown farther below, the quantity of work done will depend on whether the same net volume change is realized in a single step (by setting the external pressure to the final pressure P), or in multiple stages by adjusting the restraining pressure on the gas to successively smaller values approaching the final value of P.
Adiabatic and isothermal processes
When a gas expands, it does work on the surroundings; compression of a gas to a smaller volume similarly requires that the surroundings perform work on the gas. If the gas is thermally isolated from the surroundings, then the process is said to occur adiabatically. In an adiabatic change, q = 0, so the First Law becomes ΔU = 0 + w. Since the temperature of the gas changes with its internal energy, it follows that adiabatic compression of a gas will cause it to warm up, while adiabatic expansion will result in cooling.
In contrast to this, consider a gas that is allowed to slowly excape from a container immersed in a constant-temperature bath. As the gas expands, it does work on the surroundings and therefore tends to cool, but the thermal gradient that results causes heat to pass into the gas from the surroundings to exactly compensate for this change. This is called an isothermal expansion. In an isothermal process the internal energy remains constant and we can write the First Law as 0 = q + w, or q = –w, illustrating that the heat flow and work done exactly balance each other.
Because no thermal insulation is perfect, truly adiabatic processes do not occur. However, heat flow does take time, so a compression or expansion that occurs more rapidly than thermal equilibration can be considred adiabatic for practical purposes.
 If you have ever used a hand pump to inflate a bicycle tire, you may have noticed that the bottom of the pump barrel can get quite warm. Although a small part of this warming may be due to friction, it is mostly a result of the work you (the surroundings) are doing on the system (the gas.)
If you have ever used a hand pump to inflate a bicycle tire, you may have noticed that the bottom of the pump barrel can get quite warm. Although a small part of this warming may be due to friction, it is mostly a result of the work you (the surroundings) are doing on the system (the gas.)
Adiabatic expansion and contractions are especially important in understanding the behavior of the atmosphere. Although we commonly think of the atmosphere as homogeneous, it is really not, due largely to uneven heating and cooling over localized areas. Because mixing and heat transfer between adjoining parcels of air does not occur rapidly, many common atmospheric phenomena can be considered at least quasi-adiabatic. A more detailed exposition of this topic is given in Part 5 of this unit.
Reversible processes
From Problem Example 1 we see that when a gas expands into a vacuum (Pexternal = 0) the work done is zero. This is the minimum work the gas can do; what is the maximum work the gas can perform on the surroundings? To answer this, notice that more work is done when the process is carried out in two stages than in one stage; a simple calculation will show that even more work can be obtained by increasing the number of stages— that is, by allowing the gas to expand against a series of successively lower external pressures. In order to extract the maximum possible work from the process, the expansion would have to be carried out in an infinite sequence of infinitessimal steps. Each step yields an increment of work P ΔV which can be expressed as (RT/V) dV and integrated:
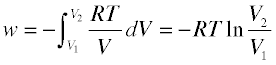 (3-5)
(3-5)
Although such a path (which corresponds to what is called a reversible process) cannot be realized in practice, it can be approximated as closely as desired.
Even though no real process can take place reversibly (it would take an infinitely long time!), reversible processes play an essential role in thermodynamics. The main reason for this is that qrev and wrev are state functions which are important and are easily calculated. Moreover, many real processes take place sufficiently gradually that they can be treated as approximately reversible processes for easier calculation.
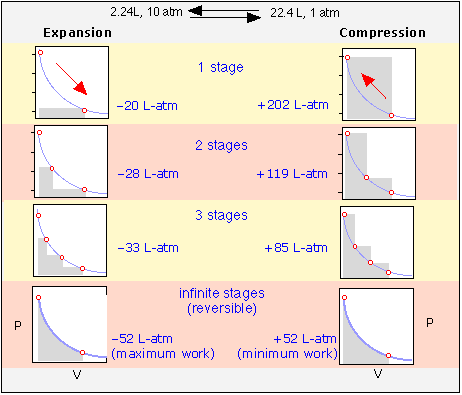 These plots illustrate the effects of various degrees of reversibility on the amount of work done when a gas expands, and the work that must be done in order to restore it to its initial state by recompressing it. The work, in each case, is proportional to the shaded area on the plot.
These plots illustrate the effects of various degrees of reversibility on the amount of work done when a gas expands, and the work that must be done in order to restore it to its initial state by recompressing it. The work, in each case, is proportional to the shaded area on the plot.
Each expansion-compression cycle leaves the gas unchanged, but in all but the one in the bottom row, the surroundings are forever altered, having expended more work in compressing the gas than was performed on it when the gas expanted.
Only when the processes are carried out in an infinite number of steps will the system and the surroundings be restored to their initial states— this is the meaning of thermodynamic reversibility.
For a chemical reaction that performs no work on the surroundings, the heat absorbed is the same as the change in internal energy: q = ΔU. But many chemical processes do involve work in one form or another:
- If the total volume of the reaction products exceeds that of the reactants, then the process performs work on the surroundings in the amount PΔV, in which P is the pressure exerted by the surroundings (usually the atmosphere) on the system.
- A reaction that drives an electrical current through an external circuit performs electrical work on the surroundings.
For an isothermal process, pressure-volume work affects the heat q
We will consider only pressure-volume work in this lesson. If the process takes place at a constant pressure, then the work is given by PΔV and the change in internal energy will be
ΔU = q – PΔV (4-1)
Bear in mind why q is so important: the heat flow into or out of the system is directly measurable. ΔU, being "internal" to the system, is not directly observable.
Thus the amount of heat that passes between the system and the surroundings is given by
q = ΔU + PΔV (4-2)
This means that if an exothermic reaction is accompanied by a net increase in volume under conditons of constant pressure, some heat additional to ΔU must be absorbed in order to supply the energy expended as work done on the surroundings if the temperature is to remain unchanged (isothermal process.)
For most practical purposes, changes in the volume of the system are only significant if the reaction is accompanied by a difference in the moles of gaseous reactants and products.
For example, in the reaction H2(g) + ½O2(g) → H2O(l), the total volume of the system decreases from that correponding to 1.5 moles of gaseous reactants to 0.5 mol of liquid water which occupies only 9 mL — a volume so small in comparison to that of the reactants that it can be neglected without significant error. So all we are really concerned with is the difference in the number of moles of gas Δng:
Δng = (0 – 1.5) mol = –1.5 mol
This corresponds to a net contraction (negative expansion) of the system, meaning that the surroundings perform work on the system.
The molar volume of an ideal gas at 25° C and 1 atm is
(298/273) × (22.4 L mol–1) = 24.5 L mol–1
Remember the sign convention: a flow of heat or performance of work that supplies energy is positive; if it consumes energy, it is negative. Thus work performed by the surroundings diminishes the energy of the surroundings (wsurr < 0) and increases the energy of the system (wsys > 0).
and the work done (by the surroundings on the system) is
(1 atm) (–1.5 mol)(24.5 L mol–1) = –36.75 L-atm.
Using the conversion factor 1 L-atm = 101.3 J, and bearing in mind that work performed on the system supplies energy to the system, the work associated solely with the volume change of the system increases its energy by
(101.3 J/L-atm)(–36.75 L-atm) = 3712 J = 3.71 kJ
About "constant" pressure and temperature processes
This terminology can be somewhat misleading unless you bear in mind that the conditions ΔP and ΔT refer to the differences between the inital and final states of the system — that is, before and after the reaction.
During the time the reaction is in progress, the temperature of the mixture will rise or fall, depending on whether the process is exothermic or endothermic. But because ΔT is a state function, its value is independent of what happens "in between" the initial state (reactants) and final state (products). The same is true of ΔV.
Enthalpy hides work and saves it too!
Because most chemical changes we deal with take place at constant pressure, it would be tedious to have to explicitly deal with the pressure-volume work details that were described above. Fortunately, chemists have found a way around this; they have simply defined a new state function that incorporates and thus hides within itself any terms relating to incidental kinds of work
(P-V, electrical, etc.)
Since both ΔP and ΔV in Eq 4-2 are state functions, then qP , the heat that is absorbed or released when a process takes place at constant pressure, must also be a state function and is known as the enthalpy change ΔH.
important ⇒ ΔH ≡ qP = ΔU + PΔV(4-3)
Since most processes that occur in the laboratory, on the surface of the earth, and in organisms do so under a constant pressure of one atmosphere, Eq 4-3 is the form of the First Law that is of greatest interest to most of us most of the time.
For systems in which no change in composition (chemical reaction) occurs, things are even simpler: to a very good approximation, the enthalpy depends only on the temperature. This means that the temperature of such a system can serve as a direct measure of its enthalpy. The functional relation between the internal energy and the temperature is given by the heat capacity measured at constant pressure:
![]() (5-1)
(5-1)
(or ΔH/ΔT if you don’t care for calculus!) An analogous quantity relates the heat capacity at constant volume to the internal energy:
![]() (5-2)
(5-2)
The difference between
CP andCV is of importance only when the volume of the system changes significantly— that is, when different numbers of moles of gases appear on either side of the chemical equation. For reactions involving only liquids and solids, Cp and Cv are for all practical purposes identical.
Heat capacity can be expressed in joules or calories per mole per degree (molar heat capacity), or in joules or calories per gram per degree; the latter is called the specific heat capacity or just the specific heat.

