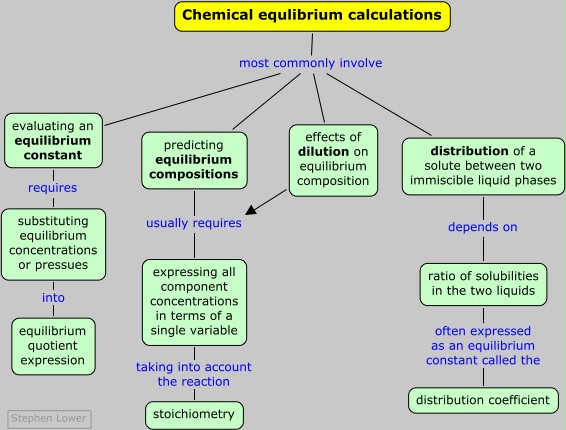
Equilibrium calculations
Some common kinds of problems
On this page:
This page presents examples that cover most of the kinds of equilibrium problems you are likely to encounter in a first-year university course.
Reading this page will not teach you how to work equilibrium problems! The only one who can teach you how to interpret, understand, and solve problems is yourself.
So don't just "read" this and think you are finished. You need to find and solve similar problems on your own. Look over the problems in your homework assignment or at the end of the appropriate chapter in a textbook, and see how they fit into the general types described below. When you can solve them without looking at the examples below, you will be well on your way!
Clearly, if the concentrations or pressures of all the components of a reaction are known, then the value of K can be found by simple substitution. Observing individual concentrations or partial pressures directly may be not always be practical, however. If one of the components is colored, the extent to which it absorbs light of an appropriate wavelength may serve as an index of its concentration. Pressure measurements are ordinarily able to measure gonly the total pressure of a gaseous mixture, so if two or more gaseous products are present in the equilibrium mixture, the partial pressure of one may need to be inferred from that of the other, taking into account the stoichiometry of the reaction.
This is by far the most common kind of equilibrium problem you will encounter: starting with an arbitrary number of moles of each component, how many moles of each will be present when the system comes to equilibrium?
The principal source of confusion and error for beginners relates to the need to determine the values of several unknowns (a concentration or pressure for each component) from a single equation, the equilibrium expression. The key to this is to make use of the stoichiometric relationships between the various components, which usually allow us to express the equilibrium composition in terms of a single variable. The easiest and most error-free way of doing this is adopt a systematic approach in which you create and fill in a small table as shown in the following problem example. You then substitute the equilibrium values into the equilibrium constant expression, and solve it for the unknown.
This very often involves solving a quadratic or higher-order equation. Quadratics can of course be solved by using the familiar quadratic formula, but it is often easier to use an algebraic or graphical approximation, and for higher-order equations this is the only practical approach. There is almost never any need to get an exact answer, since the equilibrium constants you start with are rarely known all that precisely anyway.
In the section that introduced the LeChâtelier principle, it was mentioned that diluting a weak acid such as acetic acid CH3COOH (“HAc”) will shift the dissociation equilibrium to the right:
HAc + H2O → H3O+ + Ac–
Thus a 0.10M solution of acetic acid is 1.3% ionized, while in a 0.01M solution, 4.3% of the HAc molecules will be dissociated. This is because as the solution becomes more dilute, the product [H3O+][Ac–] decreases more rapidly than does the [HAc] term. At the same time the concentration of H2O becomes greater, but because it is so large to start with (about 55.5M), any effect this might have is negligible, which is why no [H2O] term appears in the equilibrium expression.
For a reaction such as CH3COOH(l) + C2H5OH(l) → CH3COOC2H5(l) + H2O(l) (in which the water concentration does change), dilution will have no effect on the equilibrium; the situation is analogous to the way the pressure dependence of a gas-phase reaction depends on the number of moles of gaseous components on either side of the equation.
It often happens that two immiscible liquid phases are in contact, one of which contains a solute. How will the solute tend to distribute itself between the two phases? One’s first thought might be that some of the solute will migrate from one phase into the other until it is distributed equally between the two phases, since this would correspond to the maximum dispersion (randomness) of the solute. This, however, does not take into the account the differing solubilities the solute might have in the two liquids; if such a difference does exist, the solute will preferentially migrate into the phase in which it is more soluble.
For a solute S distributed between two phases a and b the process Sa = Sb is defined by the distribution law
![]()
in which Ka,b is the distribution ratio (also called the distribution coefficient) and [S]i is the solubility of the solute in the phase.
Extraction
Extraction is the chemist's term for using an immiscible solvent to recover a desired product from a liquid solution or solid material.
 In preparative chemistry it is frequently necessary to recover a desired product present in a reaction mixture by extracting it into another liquid in which it is more soluble than the unwanted substances. On the laboratory scale this operation is carried out in a separatory funnel as shown here. [image: ransirimal]
In preparative chemistry it is frequently necessary to recover a desired product present in a reaction mixture by extracting it into another liquid in which it is more soluble than the unwanted substances. On the laboratory scale this operation is carried out in a separatory funnel as shown here. [image: ransirimal]

Continuous extraction: the Soxhlet extractor
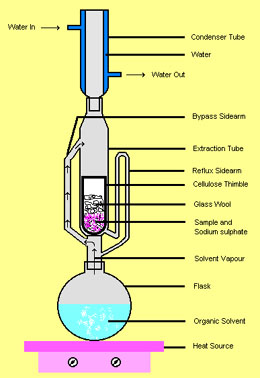 An ingenious apparatus invented by Franz von Soxhlet in 1879 has saved laboratory workers untold hours of drudgery by arranging a siphon ("bypass sidearm" in the illustration) to repeatedly send a quantity of solvent through the sample contained in a porous cellulose thimble.
An ingenious apparatus invented by Franz von Soxhlet in 1879 has saved laboratory workers untold hours of drudgery by arranging a siphon ("bypass sidearm" in the illustration) to repeatedly send a quantity of solvent through the sample contained in a porous cellulose thimble.
The samples are usually natural products such as plant materials from which something is to be extracted and concentrated. If the desired product is water-soluble, water is used as the extracting solvent; otherwise, an organic solvent is used. Once the appropriate water- or organic fraction is concentrated, the desired component can be isolated by other means.
The beauty of this glass-blower's delight is that the same initial quantity of solvent is re-used. When the solvent is boiled in the flask a the bottom, the hot vapors pass through the "bypass sidearm" up into the condenser at the top, where the condensed liquid then drips down into the reflux column and fills the "extraction tube". When the solvent level level of the upper bend of the "reflux sidearm", it starts a siphon that completely empties the extraction tube, returning the now-enriched solvent to the boiling flask.
This Wikipedia article has an excellent animation of the Soxhlet extractor.
[image]
The six Problem Examples presented above were carefully selected to span the range of problem types that students enrolled in first-year college chemistry courses are expected to be able to deal with. If you are able to reproduce these solutions on your own, you should be well prepared on this topic.
- The first step in the solution of all but the simplest equilibrium problems is to sketch out a table showing for each component the initial concentration or pressure, the change in this quantity (for example, +2x), and the equilibrium values (for example, .0036 + 2x). In doing so, the sequence of calculations required to get to the answer usually becomes apparent.
- Equilibrium calculations often involve quadratic- or higher-order equations. Because concentrations, pressures, and equilibrium constants are seldom known to a precision of more than a few significant figures, there is no need to seek exact solutions. Iterative approximations (as in Problem Example 3) or use of a graphical calculator (Problem Example 4) are adequate and convenient.
- Phase distribution equilibria play an important role in chemical separation processes on both laboratory and industrial scales. They are also involved in the movement of chemicals between different parts of the environment, and in the bioconcentration of pollutants in the food chain.