Why doesn't the electron fall into the nucleus?

The picture of electrons "orbiting" the nucleus like planets around the sun remains an enduring one, not only in popular images of the atom but also in the minds of many of us who know better. The proposal, first made in 1913, that the centrifugal force of the revolving electron just exactly balances the attractive force of the nucleus (in analogy with the centrifugal force of the moon in its orbit exactly counteracting the pull of the Earth's gravity) is a nice picture, but is simply untenable.

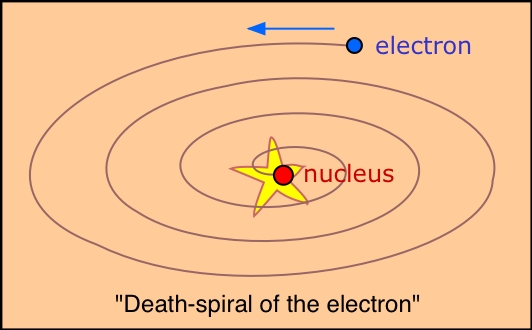An electron, unlike a planet or a satellite, is electrically charged, and it has been known since the mid-19th century that an electric charge that undergoes acceleration (changes velocity and direction) will emit electromagnetic radiation, losing energy in the process. A revolving electron would transform the atom into a miniature radio station, the energy output of which would be at the cost of the potential energy of the electron; according to classical mechanics, the electron would simply spiral into the nucleus and the atom would collapse.

Quantum theory to the rescue!

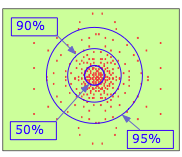By the 1920's, it became clear that a tiny object such as the electron cannot be treated as a classical particle having a definite position and velocity. The best we can do is specify the probability of its manifesting itself at any point in space. If you had a magic camera that could take a sequence of pictures of the electron in the 1s orbital of a hydrogen atom, and could combine the resulting dots in a single image, you would see something like this. Clearly, the electron is more likely to be found the closer we move toward the nucleus.

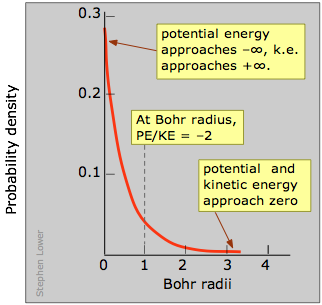This is confirmed by this plot which shows the quantity of electron charge per unit volume of space at various distances from the nucleus. This is known as a probability density plot. The per unit volume of space part is very important here; as we consider radii closer to the nucleus, these volumes become very small, so the number of electrons per unit volume increases very rapidly. In this view, it appears as if the electron does fall into the nucleus!

 

 

 

Battle of the infinities

But it doesn't stay there! As you know, the potential energy of an electron becomes more negative as it moves toward the attractive field of the nucleus; in fact, it approaches negative infinity. But because the total energy remains constant (a hydrogen atom, sitting peacefully by itself, will neither lose nor acquire energy), the loss in potential energy is compensated for by an increase in the electron's kinetic energy (sometimes referred to in this context as "confinement" energy) which determines its momentum and its effective velocity.

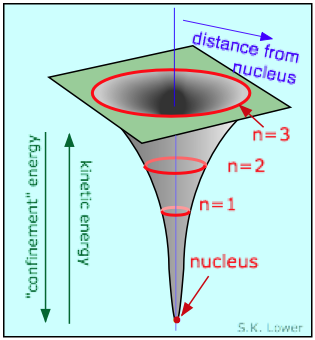So as the electron approaches the tiny volume of space occupied by the nucleus, its potential energy dives down toward minus-infinity, and its kinetic energy (momentum and velocity) shoots up toward positive-infinity. This "battle of the infinities" cannot be won by either side, so a compromise is reached in which theory tells us that the fall in potential energy is just twice the kinetic energy, and the electron dances at an average distance that corresponds to the Bohr radius.

But there is still one thing wrong with this picture; according to the Heisenberg uncertainty principle (a better term would be "indeterminacy"), a particle as tiny as the electron cannot be regarded as having either a definite location or momentum. The Heisenberg principle says that either the location or the momentum of a quantum particle such as the electron can be known as precisely as desired, but as one of these quantities is specified more precisely, the value of the other becomes increasingly indeterminate. It is important to understand that this is not simply a matter of observational difficulty, but rather a fundamental property of nature.

See here for more on the uncertainty principle

What this means is that within the tiny confines of the atom, the electron cannot really be regarded as a "particle" having a definite energy and location, so it is somewhat misleading to talk about the electron "falling into" the nucleus. (A famous physicist once suggested, not entirely in jest, that a better description of the electron would be "wavicle"!)

Probability density vs. radial probability

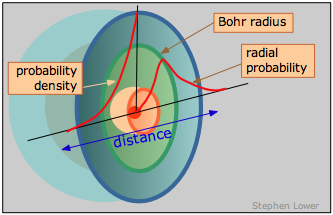We can, however, talk about where the electron has the highest probability of manifesting itself— that is, where the maximum negative charge will be found.

This is just the curve labeled "probability density"; its steep climb as we approach the nucleus shows unambiguously that the electron is most likely to be found in the tiny volume element at the nucleus. But wait! Did we not just say that this does not happen? What we are forgetting here is that as we move out from the nucleus, the number of these small volume elements situated along any radius increases very rapidly with r, going up by a factor of 4πr². So the probability of finding the electron somewhere on a given radius circle is found by multiplying the probability density by 4πr². This yields the curve you have probably seen elsewhere, known as the radial probability, that is shown on the right side of the above diagram. The peak of the radial probability for principal quantum number n = 1 corresponds to the Bohr radius.

To sum up, the probability density and radial probability plots express two different things: the first shows the electron density at any single point in the atom, while the second, which is generally more useful to us, tells us the the relative electron density summed over all points on a circle of given radius.

For more detailed descriptions of these two kinds of plots, see this McMaster U. page by Richard Bader. A very nice set of radial probability plots for several values of n in the hydrogen atom can be found near the bottom of this page.

I am grateful to Robert Harrison of U. of Tennessee-Knoxville whose suggestions led me to improve this article.

Why Doesn't the Electron Fall Into the Nucleus? Franklin Mason and Robert Richardson, J Chem. Ed. 1983 (40-42). See also the comment on this article by Werner Luck, J Chem Ed 1985 (914).

Primer on quantum theory of the atom: a quantum catechism. An elementary introduction to quantum theory in the form of a question-and-answer "primer", emphasizing the concepts with a minimum of mathematics.

For a thorough discussion of atomic structure, see the Chem1 Virtual Textbook lesson set on Atomic Structure and the Periodic Table.