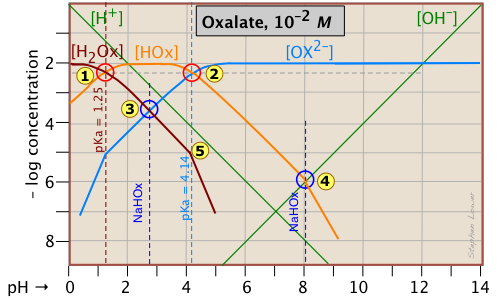

Diprotic acids are no more complicated to treat graphically than monoprotic acids-- something that definitely cannot be said for exact algebraic treatment! The above example for oxalic acid (H2Ox = HOOCCOOH) is just the superposition for separate plots of the two acid-base systems H2Ox-HOx– and HOx–-Ox2– whose pKs are 1.2 and 4.2. The system points corresponding to 0.01M solutions of pure H2A (1) and A2– (2) are determined just as in the monoprotic case. For a solution of the ampholyte NaHOx, several equilibria can be written, but the one that dominates is
2 HOx– <==> H2Ox + A2–
which leads to the approximation
[HOx–] ≈ [Ox2–]
Thus fixing the pH at about 2.7. This same result can be obtained from thewell known approximation pH = (pK1 + pK2)/2.