On this page:
The preceding page explained how the tendency of thermal energy to disperse as widely as possible is what drives all spontaneous processes, including, of course chemical reactions. We now need to understand how the direction and extent of the spreading and sharing of energy can be related to measurable thermodynamic properties of substances— that is, of reactants and products.
You will recall that when a quantity of heat q flows from a warmer body to a cooler one, permitting the available thermal energy to spread into and populate more microstates, that the ratio q/T measures the extent of this energy spreading. It turns out that we can generalize this to other processes as well, but there is a difficulty with using q because it is not a state function; that is, its value is dependent on the pathway or manner in which a process is carried out. This means, of course, that the quotient q/T cannot be a state function either, so we are unable to use it to get differences between reactants and products as we do with the other state functions. The way around this is to restrict our consideration to a special class of pathways that are described as reversible.
A change is said to occur reversibly when it can be carried out in a series of infinitessimal steps, each one of which can be undone by making a similarly minute change to the conditions that bring the change about.
For example, the reversible expansion of a gas can be achieved by reducing the external pressure in a series of infinitessimal steps; reversing any step will restore the system and the surroundings to their previous state. Similarly, heat can be transferred reversibly between two bodies by changing the temperature difference between them in infinitessimal steps each of which can be undone by reversing the temperature difference.
The most widely cited example of an irreversible change is the free expansion of a gas into a vacuum. Although the system can always be restored to its original state by recompressing the gas, this would require that the surroundings perform work on the gas. Since the gas does no work on the surrounding in a free expansion (the external pressure is zero, so PΔV = 0,) there will be a permanent change in the surroundings. Another example of irreversible change is the conversion of mechanical work into frictional heat; there is no way, by reversing the motion of a weight along a surface, that the heat released due to friction can be restored to the system.
Reversible and irreversible gas expansion and compression
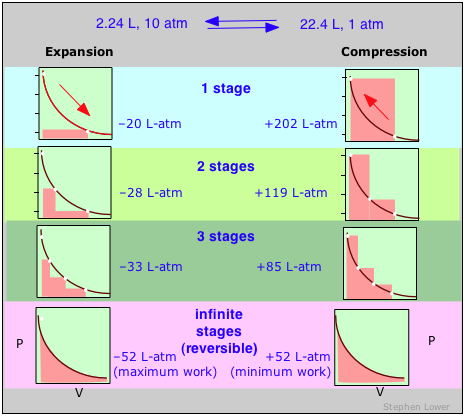 These diagrams show the same expansion and compression ±ΔV carried out in different numbers of steps ranging from a single step at the top to an "infinite" number of steps at the bottom. As the number of steps increases, the processes become less irreversible; that is, the difference between the work done in expansion and that required to re-compress the gas diminishes. In the limit of an ”infinite” number of steps (bottom), these work terms are identical, and both the system and surroundings (the “world”) are unchanged by the expansion-compression cycle. In all other cases the system (the gas) is restored to its initial state, but the surroundings are forever changed.
These diagrams show the same expansion and compression ±ΔV carried out in different numbers of steps ranging from a single step at the top to an "infinite" number of steps at the bottom. As the number of steps increases, the processes become less irreversible; that is, the difference between the work done in expansion and that required to re-compress the gas diminishes. In the limit of an ”infinite” number of steps (bottom), these work terms are identical, and both the system and surroundings (the “world”) are unchanged by the expansion-compression cycle. In all other cases the system (the gas) is restored to its initial state, but the surroundings are forever changed.
A reversible change is one carried out in such as way that, when undone, both the system and surroundings (that is, the world) remain unchanged.
Reversible = impossible: so why bother ?
It should go without saying, of course, that any process that proceeds in infinitissimal steps would take infinitely long to occur, so thermodynamic reversibility is an idealization that is never achieved in real processes, except when the system is already at equilibrium, in which case no change will occur anyway! So why is the concept of a reversible process so important?
The answer can be seen by recalling that the change in the internal energy that characterizes any process can be distributed in an infinity of ways between heat flow across the boundaries of the system and work done on or by the system, as expressed by the First Law ΔU = q + w. Each combination of q and w represents a different pathway between the initial and final states. It can be shown that as a process such as the expansion of a gas is carried out in successively longer series of smaller steps, the absolute value of q approaches a minimum, and that of w approaches a maximum that is characteristic of the particular process.
Thus when a process is carried out reversibly, the w-term in the First Law expression has its greatest possible value, and the q-term is at its smallest. These special quantities wmax and qmin (which we denote as qrev and pronounce “q-reversible”) have unique values for any given process and are therefore state functions.
Work and reversibility
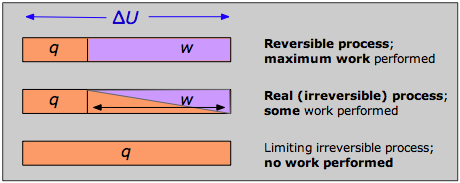 Note that the reversible condition implies wmax and qmin. The impossibility of extracting all of the internal energy as work is essentially a statement of the Second Law.
Note that the reversible condition implies wmax and qmin. The impossibility of extracting all of the internal energy as work is essentially a statement of the Second Law.
For a process that reversibly exchanges a quantity of heat qrev with the surroundings, the entropy change is defined as
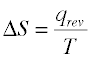 (2-1) Important!
(2-1) Important!
This is the basic way of evalulating ΔS for constant-temperature processes such as phase changes, or the isothermal expansion of a gas. For processes in which the temperature is not constant such as heating or cooling of a substance, the equation must be integrated over the required temperature range, as in Eq (2-3) further on.
...but if no real process can take place reversibly, what use is an expression involving qrev? This is a rather fine point that you should understand: although transfer of heat between the system and surroundings is impossible to achieve in a truly reversible manner, this idealized pathway is only crucial for the definition of ΔS; by virtue of its being a state function, the same value of ΔS will apply when the system undergoes the same net change via any pathway. For example, the entropy change a gas undergoes when its volume is doubled at constant temperature will be the same regardless of whether the expansion is carried out in 1000 tiny steps (as reversible as patience is likely to allow) or by a single-step (as irreversible a pathway as you can get!) expansion into a vacuum.
within a system.
This “spreading and sharing” can be spreading of the thermal energy into a larger volume of space or its sharing amongst previously inaccessible microstates of the system. The following table shows how this concept applies to a number of common processes.
system and process |
source of entropy increase of system |
| A deck of cards is shuffled, or 100 coins, initially heads up, are randomly tossed. | This has nothing to do with entropy because macro objects are unable to exchange thermal energy with the surroundings within the time scale of the process |
| Two identical blocks of copper, one at 20°C and the other at 40°C, are placed in contact. | The cooler block contains more unoccupied microstates, so heat flows from the warmer block until equal numbers of microstates are populated in the two blocks. |
| A gas expands isothermally to twice its initial volume. | A constant amount of thermal energy spreads over a larger volume of space |
| 1 mole of water is heated by 1C°. | The increased thermal energy makes additional microstates accessible. (The increase is by a factor of about 1020,000,000,000,000, 000,000,000.) |
| Equal volumes of two gases are allowed to mix. | The effect is the same as allowing each gas to expand to twice its volume; the thermal energy in each is now spread over a larger volume. |
| One mole of dihydrogen, H2, is placed in a container and heated to 3000K. | Some of the H2 dissociates to H because at this temperature there are more thermally accessible microstates in the 2 moles of H. (See the diagram relating to hydrogen microstates in the previous lesson. |
| The above reaction mixture is cooled to 300K. | The composition shifts back to virtually all H2 because this molecule contains more thermally accessible microstates at low temperatures. |
Entropy is an extensive quantity; that is, it is proportional to the quantity of matter in a system; thus 100 g of metallic copper has twice the entropy of 50 g at the same temperature. This makes sense because the larger piece of copper contains twice as many quantized energy levels able to contain the thermal energy.
Entropy and "disorder"
The late Frank Lambert contributed greatly to debunking the "entropy = disorder" myth in chemistry education. See his articles Entropy is Simple, and Teaching Entropy.
Entropy is still described, particularly in older textbooks, as a measure of disorder. In a narrow technical sense this is correct, since the spreading and sharing of thermal energy does have the effect of randomizing the disposition of thermal energy within a system. But to simply equate entropy with “disorder” without further qualification is extremely misleading because it is far too easy to forget that entropy (and thermodynamics in general) applies only to molecular-level systems capable of exchanging thermal energy with the surroundings. Carrying these concepts over to macro systems may yield compelling analogies, but it is no longer science. it is far better to avoid the term “disorder” altogether in discussing entropy.

Fig. 2-1 [source]
Yes, it happens, but it has nothing to do with thermodynamic entropy!
See Frank Lambert's page "Shuffled Cards, Messy Desks, and Disorderly Dorm Rooms — Examples of Entropy Increase? Nonsense!"
Entropy and probability
As was explained in the preceding lesson, the distribution of thermal energy in a system is characterized by the number of quantized microstates that are accessible (i.e., among which energy can be shared); the more of these there are, the greater the entropy of the system. This is the basis of an alternative (and more fundamental) definition of entropy
S = k ln Ω (2-2)
in which k is the Boltzmann constant (the gas constant per molecule, 1.38![]() 10–23 J K–1) and Ω (omega) is the number of microstates that correspond to a given macrostate of the system. The more such microstates, the greater is the probability of the system being in the corresponding macrostate. For any physically realizable macrostate, the quantity Ω is an unimaginably large number, typically around
10–23 J K–1) and Ω (omega) is the number of microstates that correspond to a given macrostate of the system. The more such microstates, the greater is the probability of the system being in the corresponding macrostate. For any physically realizable macrostate, the quantity Ω is an unimaginably large number, typically around ![]() for one mole. By comparison, the number of atoms that make up the earth is about 1050. But even though it is beyond human comprehension to compare numbers that seem to verge on infinity, the thermal energy contained in actual physical systems manages to discover the largest of these quantities with no difficulty at all, quickly settling in to the most probable macrostate for a given set of conditions.
for one mole. By comparison, the number of atoms that make up the earth is about 1050. But even though it is beyond human comprehension to compare numbers that seem to verge on infinity, the thermal energy contained in actual physical systems manages to discover the largest of these quantities with no difficulty at all, quickly settling in to the most probable macrostate for a given set of conditions.
The reason S depends on the logarithm of Ω is easy to understand. Suppose we have two systems (containers of gas, say) with S1, Ω1 and S2, Ω2. If we now redefine this as a single system (without actually mixing the two gases), then the entropy of the new system will be S = S1 + S2 but the number of microstates will be the product Ω1Ω2 because for each state of system 1, system 2 can be in any of Ω2 states. Because ln(Ω1Ω2) = ln Ω1 + ln Ω2, the additivity of the entropy is preserved.
Entropy, equilibrium, and the direction of time
If someone could make a movie showing the motions of individual atoms of a gas or of a chemical reaction system in its equilibrium state, there is no way you could determine, on watching it, whether the film is playing in the forward or reverse direction. Physicists describe this by saying that such systems possess time-reversal symmetry; neither classical nor quantum mechanics offers any clue to the direction of time.
But when a movie showing changes at the macroscopic level is being played backward, the weirdness is starkly apparent to anyone; if you see books flying off of a table top or tea being sucked back up into a teabag (or a chemical reaction running in reverse), you will immediatly know that something is wrong. At this level, time clearly has a direction, and it is often noted that because the entropy of the world as a whole always increases and never decreases, it is entropy that gives time its direction. It is for this reason that entropy is sometimes referred to as "time's arrow" (see this excellent Wikipedia article on the subject.)
But there is a problem here: conventional thermodynamics is able to define entropy change only for reversible processes which, as we know, take infinitely long to perform. So we are faced with the apparent paradox that thermodynamics, which deals only with differences between states and not the journeys between them, is unable to describe the very process of change by which we are aware of the flow of time.
A very interesting essay by Peter Coveney of the University of Wales offers a possible solution to this problem.
The direction of time is revealed to the chemist by the progress of a reaction toward its state of equilibrium; once equilibrium is reached, the net change that leads to it ceases, and from the standpoint of that particular system, the flow of time stops.
If we extend the same idea to the much larger system of the world as a whole, this leads to the concept of the "heat death of the universe" that was mentioned briefly in the previous lesson. (See here for a summary of the various interpretations of this concept.)
Energy values, as you know, are all relative, and must be defined on a scale that is completely arbitrary; there is no such thing as the absolute energy of a substance, so we can arbitrarily define the enthalpy or internal energy of an element in its most stable form at 298K and 1 atm pressure as zero.
The same is not true of the entropy; since entropy is a measure of the “dilution” of thermal energy, it follows that the less thermal energy available to spread through a system (that is, the lower the temperature), the smaller will be its entropy. In other words, as the absolute temperature of a substance approaches zero, so does its entropy.
This principle is the basis of the Third law of thermodynamics, which states that the entropy of a perfectly-ordered solid at 0° K is zero.
How entropies are measured
The absolute entropy of a substance at any temperature above 0° K must be determined by calculating the increments of heat q required to bring the substance from 0° K to the temperature of interest, and then summing the ratios q/T . Two kinds of experimental measurements are needed:
- The enthalpies associated with any phase changes the substance may undergo within the temperature range of interest. Melting of a solid and vaporization of a liquid correspond to sizeable increases in the number of microstates available to accept thermal energy, so as these processes occur, energy will flow into a system, filling these new microstates to the extent required to maintain a constant temperature (the freezing or boiling point); these inflows of thermal energy correspond to the heats of fusion and vaporization. The entropy increase associated with melting, for example, is just ΔHfusion/Tm.
- The heat capacity C of a phase expresses the quantity of heat required to change the temperature by a small amount ΔT , or more precisely, by an infinitessimal amount dT . Thus the entropy increase brought about by warming a substance over a range of temperatures that does not encompass a phase transition is given by the sum of the quantities C dT/T for each increment of temperature dT . This is of course just the integral
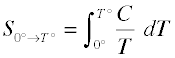 < (2-3)
< (2-3)
Because the heat capacity is itself slightly temperature dependent, the most precise determinations of absolute entropies require that the functional dependence of C on T be used in the above integral in place of a constant C . When this is not known, one can take a series of heat capacity measurements over narrow temperature increments ΔT and measure the area under each section of the curve.
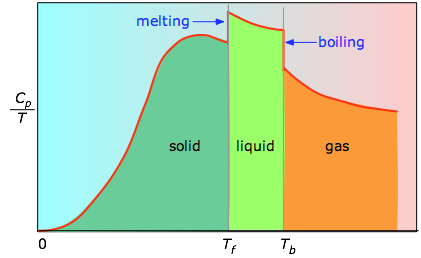 Fig 2-2 The area under each section of the plot represents the entropy change associated with heating the substance through an interval ΔT. To this must be added the enthalpies of melting, vaporization, and of any solid-solid phase changes. Values of Cp for temperatures near zero are not measured directly, but must be estimated from quantum theory.
Fig 2-2 The area under each section of the plot represents the entropy change associated with heating the substance through an interval ΔT. To this must be added the enthalpies of melting, vaporization, and of any solid-solid phase changes. Values of Cp for temperatures near zero are not measured directly, but must be estimated from quantum theory.
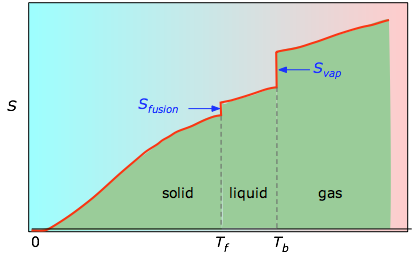 Fig 2-3 The cumulative areas from 0 K to any given temperature (taken from the experimental plot on the left) are then plotted as a function of T, and any phase-change entropies such as Svap = Hvap / Tb are added to obtain the absolute entropy at temperature T.
Fig 2-3 The cumulative areas from 0 K to any given temperature (taken from the experimental plot on the left) are then plotted as a function of T, and any phase-change entropies such as Svap = Hvap / Tb are added to obtain the absolute entropy at temperature T.
How the entropy changes with temperature
As shown in Fig 2-3 above, the entropy of a substance increases with temperature, and it does so for two reasons:
- As the temperature rises, more microstates become accessible, allowing thermal energy to be more widely dispersed. This is reflected in the gradual increase of entropy with temperature.
- The molecules of solids, liquids, and gases have increasingly greater freedom to move around, facilitating the spreading and sharing of thermal energy. Phase changes are therefore accompanied by massive and discontinuous increase in the entropy.
The standard entropy of a substance is its entropy at 1 atm pressure. The values found in tables are normally those for 298K, and are expressed in units of J K–1 mol–1. The table below shows some typical values for gaseous substances.
| He | 126 | H2 | 131 | CH4 | 186 |
| Ne | 146 | N2 | 192 | H2O(g) | 187 |
| Ar | 155 | CO | 197 | CO2 | 213 |
| Kr | 164 | F2 | 203 | C2H6 | 229 |
| Xe | 170 | O2 | 205 | n -C3H8 | 270 |
| Cl2 | 223 | n -C4H10 | 310 |
Table 1: Standard entropies of some gases at 298K, J K–1 mol–1
Note especially how the values given in this table illustrate these important points:
- Although the standard internal energies and enthalpies of these substances would be zero, the entropies are not. This is because there is no absolute scale of energy, so we conventionally set the “energies of formation” of elements in their standard states to zero. Entropy, however, measures not energy itself, but its dispersal amongst the various quantum states available to accept it, and these exist even in pure elements.
- It is apparent that entropies generally increase with molecular weight. For the noble gases, this is of course a direct reflection of the principle that translational quantum states are more closely packed in heavier molecules, allowing of them to be occupied.
- The entropies of the diatomic and polyatomic molecules show the additional effects of rotational quantum levels.
| C(diamond) | C(graphite) | Fe | Pb | Na | S(rhombic) | Si | W |
| 2.5 | 5.7 | 27.1 | 51.0 | 64.9 | 32.0 | 18.9 | 33.5 |
Table 2: Entropies of some solid elements at 298 K, J K–1 mol–1
The entropies of the solid elements are strongly influenced by the manner in which the atoms are bound to one another. The contrast between diamond and graphite is particularly striking; graphite, which is built up of loosely-bound stacks of hexagonal sheets, appears to be more than twice as good at soaking up thermal energy as diamond, in which the carbon atoms are tightly locked into a three-dimensional lattice, thus affording them less opportunity to vibrate around their equilibrium positions. Looking at all the examples in the above table, you will note a general inverse correlation between the hardness of a solid and its entropy. Thus sodium, which can be cut with a knife, has almost twice the entropy of iron; the much greater entropy of lead reflects both its high atomic weight and the relative softness of this metal. These trends are consistent with the oft-expressed principle that the more “disordered” a substance, the greater its entropy.
| solid | liquid | gas |
| 41 | 70 | 186 |
Table 3: Entropy of water at 298K,
J K–1 mol–1
Gases, which serve as efficient vehicles for spreading thermal energy over a large volume of space, have much higher entropies than condensed phases. Similarly, liquids have higher entropies than solids owing to the multiplicity of ways in which the molecules can interact (that is, store energy.)
As a substance becomes more dispersed in space, the thermal energy it carries is also spread over a larger volume, leading to an increase in its entropy.
Because entropy, like energy, is an extensive property, a dilute solution of a given substance may well possess a smaller entropy than the same volume of a more concentrated solution, but the entropy per mole of solute (the molar entropy) will of course always increase as the solution becomes more dilute.
For gaseous substances, the volume and pressure are respectively direct and inverse measures of concentration. For an ideal gas that expands at a constant temperature (meaning that it absorbs heat from the surroundings to compensate for the work it does during the expansion), the increase in entropy is given by
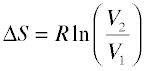 (2-4)
(2-4)
(If the gas is allowed to cool during the expansion, the relation becomes more complicated and will best be discussed in a more advanced course.)
Because the pressure of a gas is inversely proportional to its volume, we can easily alter the above relation to express the entropy change associated with a change in the pressure of a perfect gas:
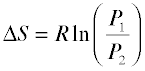 (2-5)
(2-5)
Expressing the entropy change directly in concentrations, we have the similar relation
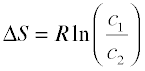 (2-6)
(2-6)
Although these equations strictly apply only to perfect gases and cannot be used at all for liquids and solids, it turns out that in a dilute solution, the solute can often be treated as a gas dispersed in the volume of the solution, so the last equation can actually give a fairly accurate value for the entropy of dilution of a solution. We will see later that this has important consequences in determining the equilibrium concentrations in a homogeneous reaction mixture.
(You are expected to be able to define and explain the significance of terms identified in green type.)
- A reversible process is one carried out in infinitessimal steps after which, when undone, both the system and surroundings (that is, the world) remain unchanged. (See the example of gas expansion-compression given above.) Although true reversible change cannot be realized in practice, it can always be approximated.
- The sum of the heat (q) and work (w) associated with a process is a state function defined by the First Law ΔU = q + w. Heat and work themselves are not state functions, and therefore depend on the particular pathway in which a process is carried out.
- As a process is carried out in a more reversible manner, the value of w approaches its maximum possible value, and q approaches its minimum possible value.
- Although q is not a state function, the quotient qrev/T is, and is known as the entropy.
- Entropy is a measure of the degree of the spreading and sharing of thermal energy within a system.
- The entropy of a substance increases with its molecular weight and complexity and with temperature. The entropy also increases as the pressure or concentration becomes smaller. Entropies of gases are much larger than those of condensed phases.
- The absolute entropy of a pure substance at a given temperature is the sum of all the entropy it would acquire on warming from absolute zero (where S=0) to the particular temperature.

 Entropy is one of the most fundamental concepts of physical science, with far-reaching consequences ranging from cosmology to chemistry. It is also widely mis-represented as a measure of "disorder", as we discuss below. The German physicist
Entropy is one of the most fundamental concepts of physical science, with far-reaching consequences ranging from cosmology to chemistry. It is also widely mis-represented as a measure of "disorder", as we discuss below. The German physicist 
 © 2003, 2007 by Stephen Lower - Simon Fraser University - Burnaby/Vancouver Canada
© 2003, 2007 by Stephen Lower - Simon Fraser University - Burnaby/Vancouver Canada 