
Introduction to crystals
Their external shapes as keys to structure
The delicately faceted surfaces of large crystals that occur in nature have always been a source of fascination and delight. In some ways they seem to represent a degree of perfection that is not apparent in other forms of matter. But in the realm of pure solid substances, crystals are the rule rather than the exception, although this may not be apparent unless they are observed under a hand-lens or a microscope.
It is remarkable that the visual examination of crystals was able to establish a fairly mature science of crystallography (applied mainly to the study of minerals) by the end of the 19th Century, even before the atomic theory of matter had been universally accepted. Today this aspect of crystallography is of importance not only to chemists and physicists, but also to geologists, amateur minerologists and "rock-hounds" who maintain some of the best Web resources on crystals.
In this lesson we will see how the external shape of a crystal can reveal much about the underlying arrangement of its constituent atoms, ions, or molecules.
 The first thing we notice about a crystal is the presence of planes — called faces — which constitute the external boundaries of the solid. Of course, any solid, including non-crystalline glass, can be carved, molded or machined to display planar faces; examples of these can be found in any "dollar store" display of costume jewelry. What distinguishes and defines a true crystal is that these faces develop spontaneously and naturally as the solid forms from a melt or from solution. The multiple faces invariably display certain geometrical relationships to one another, resulting in a symmetry that attracts our attention and delights the eye.
The first thing we notice about a crystal is the presence of planes — called faces — which constitute the external boundaries of the solid. Of course, any solid, including non-crystalline glass, can be carved, molded or machined to display planar faces; examples of these can be found in any "dollar store" display of costume jewelry. What distinguishes and defines a true crystal is that these faces develop spontaneously and naturally as the solid forms from a melt or from solution. The multiple faces invariably display certain geometrical relationships to one another, resulting in a symmetry that attracts our attention and delights the eye.
Above: sketch of a crystal of sulfur
Symmetry elements in crystals
One of the most apparent elements of this geometrical regularity are the sets of parallel faces that many crystals display. Nowhere is this more apparent than in the cubes that develop when sodium chloride crystallizes from solution. We usually think of a cubic shape in terms of the equality of its edge lengths and the 90° angles between its sides, but there is a more fundamental way of classifying shapes that chemists find very useful. This is to look at what geometric transformations (such as rotations around an axis) we can perform that leave the appearance unchanged.
Cubic symmetry
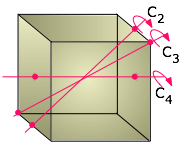 For example, you can rotate a cube 90° around an axis perpendicular to any pair of its six faces without making any apparent change to it. We say that the cube possesses three mutually perpendicular four-fold rotational axes, abbreviated C4 axes. But if you think about it, a cube can also be rotated around an axis that extends between opposite corners; in this case, it takes three 120° rotations to go through a complete circle, so these axes (also four in number) are three-fold or C3 axes. And finally, there are two-fold (C2) axes that pass diagonally through the centers of the six pairs of opposite edges.
For example, you can rotate a cube 90° around an axis perpendicular to any pair of its six faces without making any apparent change to it. We say that the cube possesses three mutually perpendicular four-fold rotational axes, abbreviated C4 axes. But if you think about it, a cube can also be rotated around an axis that extends between opposite corners; in this case, it takes three 120° rotations to go through a complete circle, so these axes (also four in number) are three-fold or C3 axes. And finally, there are two-fold (C2) axes that pass diagonally through the centers of the six pairs of opposite edges.

In addition, there are imaginary symmetry planes that mirror the portions of the cube that lie on either side of them. Three of these are parallel to the three major axes of the crystal, and an additional six pass diagonally through opposite edges.
All told, there are 13 rotational axes and 9 mirror planes (only a few of which are shown above) that define cubic symmetry. Why is this important? Although anyone can recognize a cube when they see one, it turns out that many crystals, both natural and synthetic, are for one reason or another unable to develop all of their faces equally. Thus a crystal that forms on the bottom of a container will be unable to grow any faces that project downward for the simple reason that there is no supply of ions or molecules from that direction. The same effect occurs when a mineral crystal tries to grow in contact with other solids. Finally, the presence of certain impurities that selectively adsorb to one or more faces can block the addition of more material to them, thus either completely inhibiting their formation or forcing them to grow at slower rates. These alternative shapes that can develop from a single basic crystal type are known as habits.
Crystal habits
Sodium chloride grown from pure aqueous solution forms simple cubes, but the addition of various impurities can result in habits that can be regarded as cubes that have been truncated along planes normal to some of the symmetry axes. (The same effects can sometimes be seen as a crystal slowly dissolves and material is released more rapidly from some directions than others.)
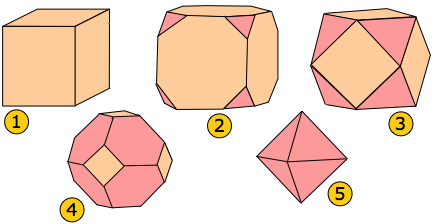
In this example, the perfect cube 1 develops triangular faces at the corners 2. If these enlarge beyond their maximum size 3, the triangular faces meet in a new set of edges that are hexagonal 4. Eventually we are left with the eight faces of what is obviously a regular octahedron 5. One might think that these five shapes bear no relationship to one another, but in fact they all possess the same set of set of symmetry elements as the simple cube and are thus various habits of the same underlying cubic structure and belong to the cubic crystal system described further below.
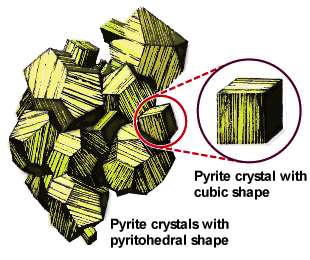 |
This sketch of a natural formation of pyrite crystals (FeS2) shows various habits of this cubic crystal growing together. [source] |
(See here for an interesting gallery of the many habits that occur in natural quartz crystals.)
Snowflakes
 Nowhere is the selective growth of certain faces more familiar to us than in snowflakes. Ice forms crystals having a hexagonal lattice structure, which in their full development would tend to form hexagonal prisms very similar to those sometimes seen in quartz. This does occasionally happen, and anyone who has done much winter mountaineering has likely seen needle-shaped prisms of ice crystals floating in the air. Under most conditions, however, the snowflake crystals we see are flattened into the beautiful fractal-like hexagonal structures that are commonly observed.
Nowhere is the selective growth of certain faces more familiar to us than in snowflakes. Ice forms crystals having a hexagonal lattice structure, which in their full development would tend to form hexagonal prisms very similar to those sometimes seen in quartz. This does occasionally happen, and anyone who has done much winter mountaineering has likely seen needle-shaped prisms of ice crystals floating in the air. Under most conditions, however, the snowflake crystals we see are flattened into the beautiful fractal-like hexagonal structures that are commonly observed.
The H2O molecules that make up the top and bottom plane faces of the prism are packed very closely and linked (through hydrogen bonding) to the molecules inside. In contrast to this, the molecules that make up the sides of the prism, and especially those at the hexagonal corners, are much more exposed, so that atmospheric H2O molecules that come into contact with most places on the crystal surface attach very loosely and migrate along it until they are able to form hydrogen-bonded attachments to these corners, thus becoming part of the solid and extending the structure along these six directions. This process perpetuates itself as the new extensions themselves acquire a hexagonal structure.
The law of constant angles
Even though a given crystal may be distorted or broken, the angles between corresponding faces remain the same. Thus you can crush a crystal underfoot or break it up with a hammer, but you will always find that the fragments possess a limited set of interfacial angles.
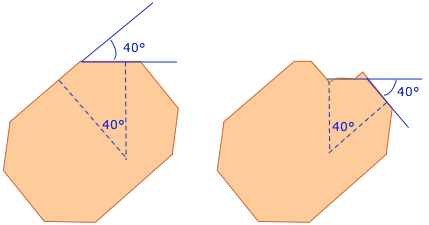
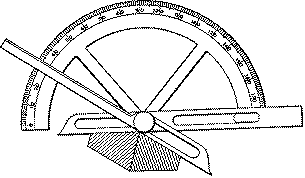 This fundamental law, discovered by Nicholas Steno in 1669, was a major key development in crystallography. About 100 years later, a protractor-like device (the contact goniometer) was invented to enable more accurate measurements than the rather crude ones that had formerly been traced out on paper.
This fundamental law, discovered by Nicholas Steno in 1669, was a major key development in crystallography. About 100 years later, a protractor-like device (the contact goniometer) was invented to enable more accurate measurements than the rather crude ones that had formerly been traced out on paper.
Cleavage planes in crystals
When a crystal is broken by applying a force in certain directions (as opposed to being pulverized by a hammer) it will often be seen to break cleanly into two pieces along what are known as cleavage planes. The new faces thus formed always correspond to the symmetry planes associated with a particular crystal type, and of course make constant angles with any other faces that may be present.
Halite (natural NaCl) crystals easily cleave along planes parallel to the cubic faces. [source] |
This sample of gypsum (CaSO4) is easily cleaved with a razor blade. [source] |
Scientific crystallography began with an accident
 Cleavage planes were first described in the late 17th century, but nothing much was thought about their significance until about a hundred years later when the Abbé Haüy accidently dropped a friend's sample of calcite and noticed how cleanly it broke. Further experimention showed that other calcite crystals, even ones of different initial shapes (habits), displayed similar rhombohedral shapes upon clevage, and that these in turn produced similar shapes when they were cleaved. This led Haüy to suggest that continued cleavages would ultimately lead to the smallest possible unit which would be the fundamental building block of the crystal. (Remember that the atomic theory of matter had not developed at this time.)
Cleavage planes were first described in the late 17th century, but nothing much was thought about their significance until about a hundred years later when the Abbé Haüy accidently dropped a friend's sample of calcite and noticed how cleanly it broke. Further experimention showed that other calcite crystals, even ones of different initial shapes (habits), displayed similar rhombohedral shapes upon clevage, and that these in turn produced similar shapes when they were cleaved. This led Haüy to suggest that continued cleavages would ultimately lead to the smallest possible unit which would be the fundamental building block of the crystal. (Remember that the atomic theory of matter had not developed at this time.)
 Haüy's elaborately drawn figures (published in 1784) showed how external faces of a crystal could be produced by stacking the units in various ways. For example, by omitting rows from a cubic stack of primal cublets, one could arrive at the various stages between the cube and the octahedra for sodium chloride that we saw earlier on this page.
Haüy's elaborately drawn figures (published in 1784) showed how external faces of a crystal could be produced by stacking the units in various ways. For example, by omitting rows from a cubic stack of primal cublets, one could arrive at the various stages between the cube and the octahedra for sodium chloride that we saw earlier on this page.
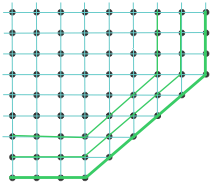
The modern interpretation of these observations replaces Haüy's primal shapes with atoms or molecules, or more generally with points in space that these define the possible locations of atoms or molecules. It is easy to see how plane faces can develop along some directions and not others if one assumes that the new faces must follow a linear sequence of points.
Formation of plane faces exhibiting constant angles |
Extended plane faces more readily form along the green and blue lines.
|
The presence of planar surfaces making only a limited number of angles defines a crystal visually, but what defines a crystal at the microscopic level is its ordered arrangement of lattice points. Although these were only revealed after the development of X-ray scattering in the early 1900's, it was Ha¨y's early sketches of tiny miniature cubes (or more generally, rhombohedra) arranged so as to replicate the shapes of various crystals that led to the concept of the crystal lattice — and this even before the atomic theory of matter had become widely accepted.
The crystal lattice
The underlying order of a crystalline solid can be represented by an array of regularly spaced points that indicate the locations of the crystal's basic structural units. This array is called a crystal lattice.
Crystal lattices are of course three-dimensional, but much of what we can say about them can be conveyed in simple two-dimensional diagrams.
Crystal lattices can be thought of as being built up from repeating units containing just a few atoms or molecules. These repeating units act much as a rubber stamp: press it on the paper, move ("translate") it by an amount equal to the lattice spacing, and stamp the paper again.
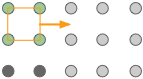
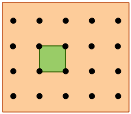
The gray circles represent a square array of lattice points. |
The orange square is the simplest unit cell that can be used to define the 2-dimensional lattice. |
Building out the lattice by moving ("translating") the unit cell in a series of steps, |
Altough real crystals do not actually grow in this manner, this process is conceptually important because it allows us to classify a lattice type in terms of the simple repeating unit that is used to "build" it. We call this shape the unit cell.
The unit cell of a crystal lattice•
Have you ever noticed how the repeating patterns on a tiled floor or on a fabric or wallpaper extend indefinitely to fill the entire area? These are known mathematically as two-dimensional lattices or nets, and they provide a nice stepping-stone to the three-dimensional lattices of crystals. Given the almost-infinite variety of designs of these kinds, it may be surprising that they can be constructed from only one of five basic unit cells:
Square Lattice: |
Parallelogram lattice |
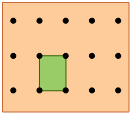
Rectangular lattice |
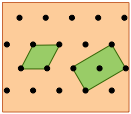
Rhombic or centered-rectangle lattice: x = y, angles neither 60° or 90°; |
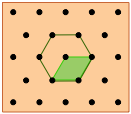
Hexagonal lattice |
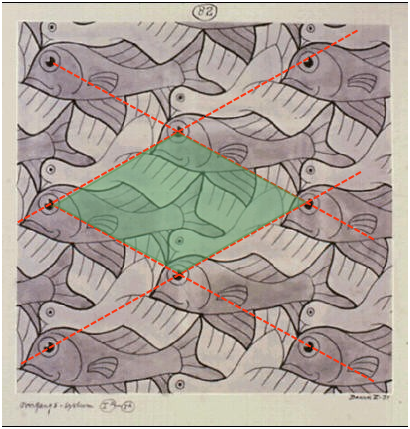 Although everyone has seen and admired the huge variety of patterns on printed fabrics or wallpapers, few are aware that these are all based on one of five types of two-dimensional "unit cells" (such as the rhombic ones superimposed on this Escher print) that form the basis for these infinitely-extendable patterns. One of the most remarkable uses of this principle is in the work of the Dutch artist Maurits Escher (1888-1972).
Although everyone has seen and admired the huge variety of patterns on printed fabrics or wallpapers, few are aware that these are all based on one of five types of two-dimensional "unit cells" (such as the rhombic ones superimposed on this Escher print) that form the basis for these infinitely-extendable patterns. One of the most remarkable uses of this principle is in the work of the Dutch artist Maurits Escher (1888-1972).
Construct your own repeating designs online: Escher Web Sketch
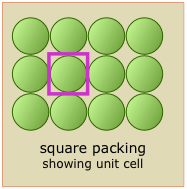
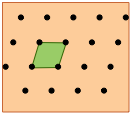
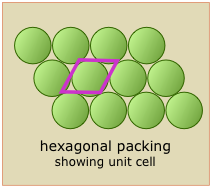 Shown here are two-dimensional views of the unit cells for two very common types of crystal lattices, one having cubic symmetry and the other being hexagonal. Although we could use a hexagon for the second of these lattices, the rhombus is preferred because it is simpler.
Shown here are two-dimensional views of the unit cells for two very common types of crystal lattices, one having cubic symmetry and the other being hexagonal. Although we could use a hexagon for the second of these lattices, the rhombus is preferred because it is simpler.
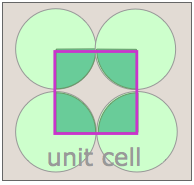 Notice that in both of these lattices, the corners of the unit cells are centered on a lattice point. This means that an atom or molecule located on this point in a real crystal lattice is shared with its neighboring cells. As is shown more clearly here for a two-dimensional square-packed lattice, a single unit cell can claim "ownership" of only one-quarter of each molecule, and thus "contains" 4 × ¼ = 1 molecule.
Notice that in both of these lattices, the corners of the unit cells are centered on a lattice point. This means that an atom or molecule located on this point in a real crystal lattice is shared with its neighboring cells. As is shown more clearly here for a two-dimensional square-packed lattice, a single unit cell can claim "ownership" of only one-quarter of each molecule, and thus "contains" 4 × ¼ = 1 molecule.
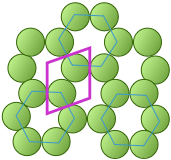
The unit cell of the graphite form of carbon is also a rhombus, in keeping with the hexagonal symmetry of this arrangement.Notice that to generate this structure from the unit cell, we need to shift the cell in both the x- and y- directions in order to leave empty spaces at the correct spots. We could alternatively use regular hexagons as the unit cells, but the x+y shifts would still be required, so the simpler rhombus is usually preferred.
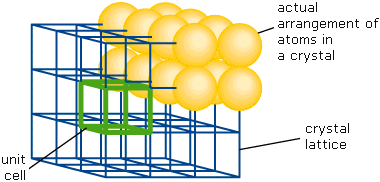 This image nicely illustrates the relations between the unit cell, the lattice structure, and the actual packing of atoms in a typical crystal.
This image nicely illustrates the relations between the unit cell, the lattice structure, and the actual packing of atoms in a typical crystal.
[source]
Crystal systems and Bravais lattices
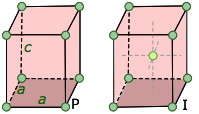
We saw above that five basic cell shapes can reproduce any design motif in two dimensions. If we go to the three-dimensional world of crystals, there are just seven possible basic lattice types, known as crystal systems, that can produce an infinite lattice by successive translations in three-dimensional space so that each lattice point has an identical environment. Each system is defined by the relations between the axis lengths and angles of its unit cell. For example, if the three edge lengths are identical and all corner angles are 90°, a crystal belongs to the cubic system.
The simplest possible cube is defined by the eight lattice points at its corner, but variants are also possible in which additional lattice points exist in the faces ("face-centered cubic") or in the center of the cube ("body-centered cubic"). If variants of this kind are taken into account, the total number of possible lattices is fourteen; these are known as the fourteen Bravais lattices.
| crystal system | Bravais lattices (P = primitive, I= body-centered, F = face-centered) |
|---|---|
cubic a = b = c |
|
tetragonal a = b ≠ c |
 A cube that has been extended in one direction, creating a unique c-axis. An F cell would simply be a network of joined I cells. A cube that has been extended in one direction, creating a unique c-axis. An F cell would simply be a network of joined I cells. |
orthorhombic a ≠ b ≠ c |
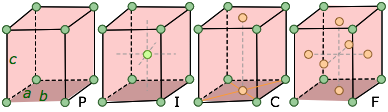 Three unequal axes at right angles. The "C" form has atoms in the two faces that cut the c-axis. |
hexagonal a = b ≠ c |
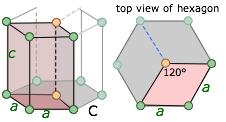 Just as in the 2-dimensional examples given above, the unit cell of the hexagonal lattice has a rhombic cross-section; the entire hexagonal unit is built from three of these rhombic prisms. |
trigonal (rhombohedral) a = b = c |
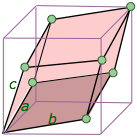 Think of this as a cube that has been skewed or distorted to one side so that opposite faces remain parallel to each other. This can also be regarded as a special case of the hexagonal system, and is often classified as such by U.S. minerologists who recognize only six crystal systems. The rhombohedral form of the hexagonal system is difficult to visualize; Steven Dutch's U. Wisconson page does an excellent job. Think of this as a cube that has been skewed or distorted to one side so that opposite faces remain parallel to each other. This can also be regarded as a special case of the hexagonal system, and is often classified as such by U.S. minerologists who recognize only six crystal systems. The rhombohedral form of the hexagonal system is difficult to visualize; Steven Dutch's U. Wisconson page does an excellent job. |
monoclinic a ≠ b ≠ c |
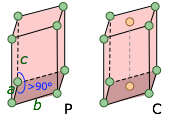 Two 90° angles, one >90°, with all sides of different lengths. A C cell (also seen in the orthorhombic class) has additional points in the center of each end. Monoclinic I and F cells can be constructed from C cells. Two 90° angles, one >90°, with all sides of different lengths. A C cell (also seen in the orthorhombic class) has additional points in the center of each end. Monoclinic I and F cells can be constructed from C cells. |
triclinic a ≠ b ≠ c |
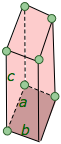 This is the most generalized of the crystal systems, with all lengths and angles unequal, and no right angles. This is the most generalized of the crystal systems, with all lengths and angles unequal, and no right angles. |
Get the Bravais Lattice Song by W.F. Smith
Lines and planes in unit cells: the Miller index
In any kind of repeating pattern, it is useful to have a convenient way of specifying the orientation of elements relative to the unit cell. This is done by assigning to each such element a set of integer numbers known as its Miller index.
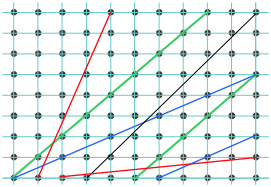
Indexing lines in two-dimensions
>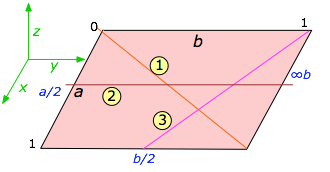 To understand indexing, it will be easier to begin with a unit cell plane that we are viewing from above, along the [invisible] z-axis. The drawing shows such a plane with three lines crossing it at various slopes. The index of each line is found by first determining the points where it intersects the x and y axes as fractions of the unit cell parameters a and b. Thus in the above example:
To understand indexing, it will be easier to begin with a unit cell plane that we are viewing from above, along the [invisible] z-axis. The drawing shows such a plane with three lines crossing it at various slopes. The index of each line is found by first determining the points where it intersects the x and y axes as fractions of the unit cell parameters a and b. Thus in the above example:
- Line
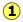 starts at the origin and extends to the lower right-hand corner which coresponds to intersections of the x axis at one unit cell length of both a and b — that is, at 1×a and 1×b. We can abbreviate this set of intersections as [1,1].
starts at the origin and extends to the lower right-hand corner which coresponds to intersections of the x axis at one unit cell length of both a and b — that is, at 1×a and 1×b. We can abbreviate this set of intersections as [1,1]. - Line
 intersects the x axis at one-half the unit cell distance a, or at a/2. This line is parallel to the y axis, so it never intersects it; this is mathematically the same as saying that it intersects it at infinity, or in terms of unit cell increments, at ∞×b. We can describe this line in terms of the unit cell intercepts by the pair of values [½,∞].
intersects the x axis at one-half the unit cell distance a, or at a/2. This line is parallel to the y axis, so it never intersects it; this is mathematically the same as saying that it intersects it at infinity, or in terms of unit cell increments, at ∞×b. We can describe this line in terms of the unit cell intercepts by the pair of values [½,∞]. - Line
 starts at the upper right corner of the cell which corresponds to the coordinates (0,1), but this is equivalent to the origin (0,0) of the neighboring unit cell on the right. So in terms of our coordinate system (which repeats for each unit cell), this line extends in the negative-y direction and intersects this axis at –b/2. The x-intercept is a. These intercepts correspond to [1,–2].
starts at the upper right corner of the cell which corresponds to the coordinates (0,1), but this is equivalent to the origin (0,0) of the neighboring unit cell on the right. So in terms of our coordinate system (which repeats for each unit cell), this line extends in the negative-y direction and intersects this axis at –b/2. The x-intercept is a. These intercepts correspond to [1,–2].
The Miller indices of the lines are given by the reciprocals of these values:
| Line 1 [1,1] → (11) | Line 2 [½,∞] → (20) | Line 3 [1,–2] → 1,2) |
Miller indices are written in parentheses with no spaces between numbers. Negative values are indicated by an overbar as in .
Indexing planes in three-dimensions
We proceed in exactly the same way, except that we now have 3-digit Miller indices corresponding to the axes a, b and c.
 It is important to note that multiple parallel planes that repeat at the same interval have identical Miller indices. This simply reflects the fact that we can repeat the coordinate axes at any regular interval.
It is important to note that multiple parallel planes that repeat at the same interval have identical Miller indices. This simply reflects the fact that we can repeat the coordinate axes at any regular interval.
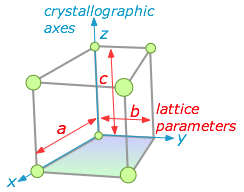
Identifying crystal faces
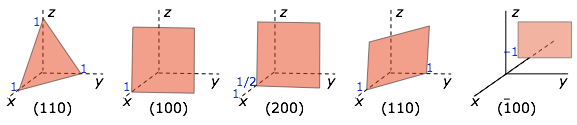
We mentioned previously that the plane faces of crystals are their most important visually-distinctive property, so it is important to have a convenient way of referring to any given face. First, we define a set of reference directions (x,y,z) which are known as the crystallographic axes. In most cases these axes correspond to directions that are fairly apparent on visual examination of one or more crystals of a given kind. They are parallel to actual or possible edges of the crystal, and they are not necessarily orthogonal. We now know, as Haüy first suggested, that these directions correspond to rows of lattice points in the underlying structure of the crystal.
We also define three lattice parameters (a,b,c) which mark out the boundaries of the unit cell along the crystallographic axes.
The index of a particular face is determined by the fractional values of (a,b,c) at which the face intersects the axes (x,y,z). Study the examples shown below for three different habits of a cubic lattice.
For a much more thorough treatment of this topic, see this page at Stephen Nelson's Tulane University Web site. The figures here are adapted from some of his. Another useful source is the page Lattice Planes and Miller Indices from Cambridge Universiy.
Below is a more complicated example of one particular habit of an orthorhombic crystal. The figure at the right shows how the (113) face is indexed.
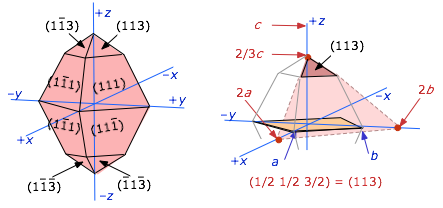
In this case, the plane at the top of the crystal is extended downward to the (x,y) plane. This extended plane cuts the (x,y,z) axes at (2a, 2b, 2/3c). The corresponding inverses would be (½,½,3/2). In order to make them into proper Miller indices (which should always be integers) we multiply everything by 2, yielding (113).
Why do Miller indices use mostly small numbers?
It is remarkable that the faces that bound real crystals generally have small Miller indices. The low values for the indices suggest that a given lattice plane has a hgh density of lattice points per unit area, a logical consquence of each molecule being surrounded and held by its closely-packed neighbors. In the 2-dimensional projection below, compare the facial lattice-point density in the (11) plane with that of the (31) plane.
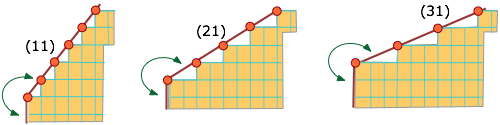
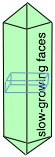 Crystals with a single long unit-cell axis tend to form planes with the long axis normal to the plane, so that the major faces of the crystal are planes containing the short-axis translations. Similarly, crystals with a single, short unit-cell axis tend to be needles. The main faces, on the sides of the needles, contain the short lattice translation — a high density of lattice points. In general, it is found that crystals have linear dimensions that mirror the reciprocals of the lattice parameters.
Crystals with a single long unit-cell axis tend to form planes with the long axis normal to the plane, so that the major faces of the crystal are planes containing the short-axis translations. Similarly, crystals with a single, short unit-cell axis tend to be needles. The main faces, on the sides of the needles, contain the short lattice translation — a high density of lattice points. In general, it is found that crystals have linear dimensions that mirror the reciprocals of the lattice parameters.
Factors affecting crystal growth habits
Faces having a lower density of lattice points (as in the (31) face shown above) can acquire new layers more rapidly, and thus grow more rapidly than faces having a high lattice-point density.
The faces that can potentially develop in a crystal are determined entirely by the symmetry properties of the underlying lattice. But the faces that actually develop under specific conditions — and thus the overall shape of the crystal — is determined by the relative rates of growth of the various faces. The slower the growth rate, the larger the face.
This relation can be understood by noting that faces that grow normal to shorter unit cell axes (as in the needle-shaped crystal shown above) present a larger density of lattice points to the surface (that is, more points per unit surface area.) This means that more time is required for diffusion of enough new particles to build out a new layer on such a surface.
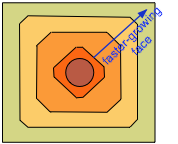 An interesting experiment is to grind a large crystal of salt into a spherical shape and immerse it in a saturated solution of sodium chloride. At first, the most disturbed and exposed parts on the surface dissolve, revealing a large variety of underlying plane faces. As growth resumes, the smaller of these are rapidly replaced by larger faces. Eventually, the fast-growing faces eliminate themselves and the high-lattice point density faces that correspond to the sides of the cube win out.
An interesting experiment is to grind a large crystal of salt into a spherical shape and immerse it in a saturated solution of sodium chloride. At first, the most disturbed and exposed parts on the surface dissolve, revealing a large variety of underlying plane faces. As growth resumes, the smaller of these are rapidly replaced by larger faces. Eventually, the fast-growing faces eliminate themselves and the high-lattice point density faces that correspond to the sides of the cube win out.
In addition to these structural effects, the conditions under which a crystal is grown can affect its habit. Temperature, degree of supersaturaton, nature of the solvent all have their effects, and these may affect the growth of different faces in different ways.
The presence of impurities in the solution can radically alter the habit of a crystal, as seen in the following table for the growth of sodium chloride:
| no impurity | Fe(CN)64– | formamide | Pb2+, Cd2+ | polyvinyl alcohol |
|---|---|---|---|---|
| cubes | dendrites | octahedra | large crystals | needles |
These effects presumably come about because these substances preferentially adsorb to certain faces, impeding their growth.
For more on this topic, see this page from the Lappeenranta U. (Finland)
and this Google Books excerpt.



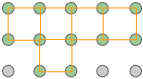
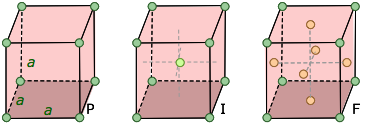 The F cell corresponds to closest cubical packing, a very common and important structure.
The F cell corresponds to closest cubical packing, a very common and important structure.