On this page:
In this unit we introduce a new thermodynamic function, the free energy, which turns out to be the single most useful criterion for predicting the direction of a chemical reaction and the composition of the system at equilibrium.
As we will explain near the bottom of this page, the term "free energy", although still widely used, is rather misleading, so we will ofen refer to it as the "Gibbs function" or "Gibbs energy"
In the previous lesson we saw that it is the sum of the entropy changes of the system and surroundings that determines whether a process will occur spontaneously. In chemical thermodynamics we prefer to focus our attention on the system rather than the surroundings, and would like to avoid having to calculate the entropy change of the surroundings explicity. The free energy enables us to do this for changes that occur at a constant temperature and pressure (the Gibbs free energy) or constant temperature and volume (the Helmholtz free energy.)
We will deal only with the Gibbs free energy in this course. The Helmholtz free energy is of interest mainly to chemical engineers (whose industrial-scale processes are often confined to tanks and reactors of fixed volume) and some geochemists whose interest is centered on the chemistry that occurs deep within the earth's surface.
The Gibbs [free] energy (also known as the Gibbs function) is defined as
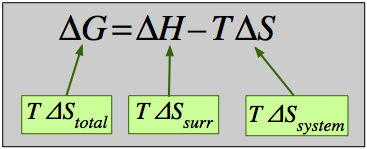
G = H – T S(4-1)
in which S refers to the entropy of the system. Since H, T and S are all state functions, so is G. Thus for any change in state, we can write the extremely important relation
ΔG = ΔH – T ΔS(4-2) Must know this!
How does this simple equation encompass the entropy change of the world ΔStotal, which we already know is the sole criterion for spontaneous change? Starting with the definition
ΔStotal = ΔSsurr + ΔSsys(4-3)
we would first like to get rid of ΔSsurr. How can a chemical reaction (a change in the system) affect the entropy of the surroundings? Because most reactions are either exothermic or endothermic, they are accompanied by a flow of heat qp across the system boundary. The enthalpy change of the reaction ΔH is defined as the flow of heat into the system from the surroundings when the reaction is carried out at constant pressure, so the heat withdrawn from the surroundings will be –qp which will cause the entropy of the surroundings to change by –qp / T = –ΔH/T. We can therefore rewrite Eq 4-3 as
ΔStotal = (– ΔH/T) + ΔSsys (4-4)
Multiplying through by –T , we obtain
–T ΔStotal = ΔH – T ΔSsys(4-5)
which expresses the entropy change of the world in terms of thermodynamic properties of the system exclusively. If –TΔStotal is denoted by ΔG, then we have Eq. 4-2 which defines the Gibbs [free] energy change for the process.
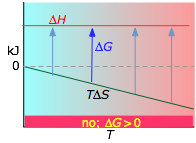
 Some textbooks and teachers say that the free energy, and thus the spontaniety of a reaction, depends on both the enthalpy and entropy changes of a reaction, and they sometimes even refer to reactions as "energy driven" or "entropy driven" depending on whether ΔH or the TΔS term dominates.This is technically correct but misleading because it disguises the important fact that ΔStotal, which this equation expresses in an indirect way, is the only criterion of spontaneous change.
Some textbooks and teachers say that the free energy, and thus the spontaniety of a reaction, depends on both the enthalpy and entropy changes of a reaction, and they sometimes even refer to reactions as "energy driven" or "entropy driven" depending on whether ΔH or the TΔS term dominates.This is technically correct but misleading because it disguises the important fact that ΔStotal, which this equation expresses in an indirect way, is the only criterion of spontaneous change.
From the foregoing, you should convince yourself that G will decrease in any process occurring at constant temperature and pressure which is accompanied by an overall increase in the entropy. (The constant temperature is a consequence of the temperature and the enthalpy appearing in the preceding equation 4-5.) Since most chemical and phase changes of interest to chemists take place under such conditions, the Gibbs energy is the most useful of all the thermodynamic properties of a substance, and (as we shall see in the lesson that follows this one) it is closely linked to the equilibrium constant.
ΔG determines the direction and extent of chemical change
The importance of the Gibbs function can hardly be over-stated: it serves as the single master variable that determines whether a given chemical change is thermodynamically possible. Thus if the free energy of the reactants is greater than that of the products, the entropy of the world will increase when the reaction takes place as written, and so the reaction will tend to take place spontaneously. Conversely, if the free energy of the products exceeds that of the reactants, then the reaction will not take place in the direction written, but it will tend to proceed in the reverse direction.
In a spontaneous change, Gibbs energy always decreases and never increases.
This of course reflects the fact that the entropy of the world behaves in the exact opposite way (owing to the negative sign in the TΔS term). Recalling the example of the freezing of water we presented in the previous lesson
H2O(liquid) → H2O (ice)
water below its freezing point undergoes a decrease in its entropy, but the heat released into the surroundings more than compensates for this, so the entropy of the world increases, the free energy of the H2O diminishes, and the process proceeds spontaneously.
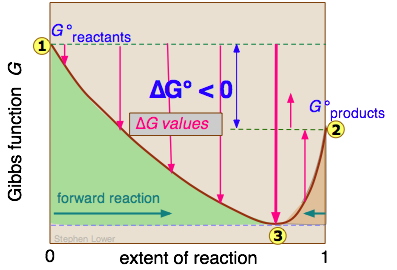
An important consequence of the one-way downward path of the free energy is that once it reaches its minimum possible value, net change comes to a halt. This, of course, represents the state of chemical equilbrium.
These relations are nicely summarized as follows:
| ΔG < 0 | reaction can spontaneously proceed to the right: A → B |
| ΔG > 0 | reaction can spontaneously proceed to the left: A ← B |
| ΔG = 0 | the reaction is at equilibrium; the quantities of A and B will not change |
This might seem strange, given the key importance ΔG in determining whether or not a reaction will take place in a given direction. It turns out, however, that it is almost never necessary to explicitly evaluate ΔG. As we will show in the lesson that follows this one, it is far more convenient to work with the equilibrium constant of a reaction, within which ΔG is "hidden". This is just as well, because for most reactions (those that take place in solutions or gas mixtures) the value of ΔG depends on the proportions of the various reaction components in the mixture; it is not a simple sum of the "products minus reactants" type, as is the case with ΔH. More on this in the next lesson!
The important role of temperature
Recalling the condition for spontaneous change
ΔG = ΔH – TΔS < 0
it is apparent that the temperature dependence of ΔG depends almost entirely on the entropy change associated with the process. (We say "almost" because the values of ΔH and ΔS are themselves slightly temperature dependent; both gradually increase with temperature). In particular, notice that in the above equation the sign of the entropy change determines whether the reaction becomes more or less spontaneous as the temperature is raised.
For any given reaction, the sign of ΔH can also be positive or negative. This means that there are four possibilities for the influence that temperature can have on the spontaniety of a process:
- Case 1: ΔH < 0 and ΔS > 0
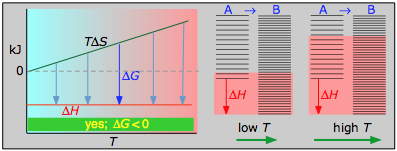
- Under these conditions, both the ΔH and TΔS terms will be negative, so ΔG will be negative regardless of the temperature. Anexothermic reaction whose entropy increases will be spontaneous at all temperatures.
- Case 2: ΔH < 0 and ΔS < 0
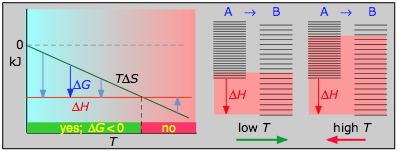 If the reaction is sufficiently exothermic it can force ΔG negative only at temperatures below which |TΔS| < |ΔH|. This means that there is a temperature T = ΔH / ΔS at which the reaction is at equilibrium; the reaction will only proceed spontaneously below this temperature. The freezing of a liquid or the condensation of a gas are the most common examples of this condition.
If the reaction is sufficiently exothermic it can force ΔG negative only at temperatures below which |TΔS| < |ΔH|. This means that there is a temperature T = ΔH / ΔS at which the reaction is at equilibrium; the reaction will only proceed spontaneously below this temperature. The freezing of a liquid or the condensation of a gas are the most common examples of this condition.
- Case 3: ΔH > 0 and ΔS > 0
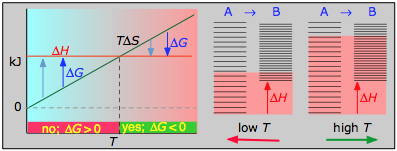 This is the reverse of the previous case; the entropy increase must overcome the handicap of an endothermic process so that TΔS > ΔH. Since the effect of the temperature is to "magnify" the influence of a positive ΔS, the process will be spontaneous at temperatures above T = ΔH / ΔS. (Think of melting and boiling.)
This is the reverse of the previous case; the entropy increase must overcome the handicap of an endothermic process so that TΔS > ΔH. Since the effect of the temperature is to "magnify" the influence of a positive ΔS, the process will be spontaneous at temperatures above T = ΔH / ΔS. (Think of melting and boiling.)
- Case 4: ΔH > 0 and ΔS < 0
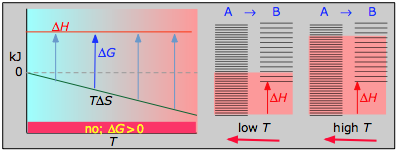 With both ΔH and ΔS working against it, this kind of process will not proceed spontaneously at any temperature. Substance A always has a greater number of accessible energy states, and is therefore always the preferred form.
With both ΔH and ΔS working against it, this kind of process will not proceed spontaneously at any temperature. Substance A always has a greater number of accessible energy states, and is therefore always the preferred form.
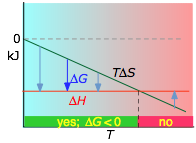
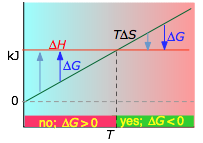
About the above diagrams
The plots on the left are the important ones; don't try to memorize them, but make sure you understand and can explain or reproduce them for a given set of ΔH and ΔS.
- Their most important differentiating features are the position of the ΔH line (above or below the is TΔS line), and the slope of the latter, which of course depends on the sign of ΔS.
- The reaction A → B will occur spontaneously only when ΔG is negative (blue arrows pointing down.)
- Owing to the slight temperature dependence of ΔS, the TΔS plots are not quite straight lines as shown here. Similarly, the lines representing ΔH are even more curved.
The other two plots on each diagram are only for the chemistry-committed.
- Each pair of energy-level diagrams depicts the relative spacing of the microscopic energy levels in the reactants and products as reflected by the value of ΔS°. (The greater the entropy, the more closely-spaced are the quantized microstates.)
- The red shading indicates the range of energy levels that are accessible to the system at each temperature. The spontaneous direction of the reaction will always be in the direction in which the red shading overlaps the greater number of energy levels, resulting in the maximum dispersal of thermal energy.
- Note that the vertical offsets correspond to ΔH° for the reaction.
- Never forget that it is the ability of thermal energy to spread into as many of these states as possible that determines the tendency of the process to take place. None of this is to scale, of course!
The maximum work
As we explained in Part 2, the two quantities qrev (qmin) and wmax associated with reversible processes are state functions. We gave the quotient qrev /T a new name, the entropy. What we did not say is that wmax also corresponds to the free energy.
The Gibbs energy is the maximum useful work (excluding PV work associated with volume changes of the system) that a system can do on the surroundings when the process occurs reversibly at constant temperature and pressure.
This work is done at the expense of the internal energy of the system, and whatever part of that is not extracted as work is exchanged with the surroundings as heat; this latter quantity will have the value –TΔS .
Reminder: what do we mean by "standard"?
You have already been introduced to the terms such as ΔU° and ΔH° in which the ° sign indicates that all components (reactants and products) are in their standard states. This concept of standard states is especially important in the case of the free energy, so let's take a few moments to review it.
For most practical purposes (and certainly for this course), the following definitions are good enough:
- gases: 1 atmosphere partial pressure
- pure liquids: the liquid under a total (hydrostatic) pressure of 1 atm.
- solutes: an effective concentration of 1 mol L–1 (1 mol dm–3). ("Effective" concentrations approach real concentrations as the latter approach zero; for practical purposes, these can be considered identical at real concentrations smaller than about 10–4 molar.)
- solids: the pure solid under 1 atm pressure
Note also that
- There is actually no "standard temperature", but because most thermodynamics tables list values for 298.15 K (25° C), this temperature is usually implied.
- These same definitions apply to standard enthalpies and internal energies.
- Don't confuse these thermodynamic standard states with the "standard temperature and pressure" (STP) widely employed in gas law calculations.
Defining ΔG° and ΔGf°
In order to make use of Gibbs energies to predict chemical changes, we need to know the free energies of the individual components of the reaction. For this purpose we can combine the standard enthalpy of formation and the standard entropy of a substance to get its standard free energy of formation
ΔGf° = ΔHf° – TΔSf°(4-6)
and then determine the standard Gibbs energy of the reaction according to
ΔG° = Σ ΔGf°(products)– Σ ΔGf°(reactants)(4-7) Must know this!
As with standard heats of formation, the standard free energy of a substance represents the free energy change associated with the formation of the substance from the elements in their most stable forms as they exist under the standard conditions of 1 atm pressure and 298K. Standard Gibbs free energies of formation are normally found directly from tables. Once the values for all the reactants and products are known, the standard Gibbs free energy change for the reaction is found by Eq 4-7.
Most tables of thermodynamic values list ΔGf°'s for common substances. They can, of course, always be found from values of ΔHf° and ΔSf°.
Find the standard Gibbs energy change for the reaction
CaCO3(s) → CaO(s)+ CO2(g)
The ΔGf° values for the three components of this reaction system are CaCO3(s): –1128 kJ mol–1, CaO(s): –603.5 kJ mol–1, CO2(g): –137.2 kJ mol–1.
Solution: Substituting into Eq. 4-7, we have
ΔG° = (–603.5 –137.2) – (–1128) kJ mol–1 = +387.3 kJ mol–1 indicating that the process is not spontaneous under standard conditions (i.e., solid calcium carbone will not form solid calcium oxide and CO2 at 1 atm partial pressure at 25° C.
Comment: This reaction is carried out on a huge scale to manufacture cement, so it is obvious that the process can be spontaneous under different conditions.
The practical importance of the Gibbs energy is that it allows us to make predictions based on the properties (ΔG° values) of the reactants and products themselves, eliminating the need to experiment. But bear in mind that while thermodynamics always correctly predicts whether a given process can take place (is spontaneous in the thermodynamic sense), it is unable to tell us if it will take place at an observable rate.
When thermodynamics says "no", it means exactly that. When it says "yes", it means "maybe".
The reaction ½ O2(g) + H2(g) → H2O(l) is used in fuel cells to produce an electrical current. The reaction can also be carried out by direct combustion.
Thermodynamic data: molar entropies in J mol–1 K–1: O2(g) 205.0; H2(g)130.6; H2O(l) 70.0; H2O(l) ΔH°f = –285.9 kJ mol–1.
Use this information to find
a) The amount of heat released when the reaction takes place by direct combustion;
b) The amount of electrical work the same reaction can perform when carried out in a fuel cell at 298K under reversible condtions;
c) The amount of heat released under the same conditions.
Solution: First, we need to find ΔH° and ΔS° for the process. Recalling that the standard enthalpy of formation of the elements is zero, ΔH° = ΔH°f(products) – ΔH°f(reactants) = –285.9 kJ mol–1 – 0 = –285.9 kJ mol–1.
Similarly, ΔS° = S°f(products) – S°f(reactants) = (70.0) – (½×205.0 + 130.6) = –163 J K–1mol–1
a) When the hydrogen and oxygen are combined directly, the heat released will be ΔH° = –285.9 kJ mol–1.
b) The maximum electrical work the fuel cell can perform is given by ΔG° = ΔH° – TΔS° = –285.9 kJ mol–1 – (298 K)(–163 JK–1mol–1) = –237.2 kJ mol–1.
c) The heat released in the fuel cell reaction is the difference between the enthalpy change (the total energy available) and the reversible work that was expended: ΔH° – ΔG°= TΔS° = (298 K)(–163 JK–1mol–1) = –48800 J mol–1 = –48.8 kJ mol–1.
In this reaction, 1.5 moles of gas disappear, to be replaced by 18 mL (1 mole) of water. The system undergoes a marked contraction in which the atmosphere performs pressure-volume work on the system. But this PV work is the "non-useful" work that is not included in the ΔG value.
The foregoing example illustrates an important advantage of fuel cells. Although direct combustion of a mole of hydrogen gas yields more energy than is produced by the same net reaction within the fuel cell, the latter, in the form of electrical energy, can be utilized at nearly 100-percent energy efficiency by a motor or some other electrical device. If the thermal energy released by direct combustion were supplied to a heat engine, second-law considerations would require that at least half of this energy be "wasted" to the surroundings.
The apparent similarity of the terms ΔG, ΔG° and ΔGf° makes it easy to overlook the distinctions between them and is a major source of confusion and error for students (and sometimes even for teachers!) Although these terms were discussed above, it might be useful to summarize and expand upon these distinctions.
The most important thing to remember is that the terms ΔG° and ΔGf° refer to single, specific chemical changes in which all components (reactants and products) are in their standard states.
Standard Gibbs energies of formation
The ΔGf° of a substance, like ΔHf°, refers to the reaction in which that substance is formed from the elements as they exist in their most stable forms at 1 atm pressure and (usually) 298K. Both of these Δ terms are by definition zero for the elements in their standard states.
There are only a few common cases in which this might create some ambiguity:
| stable form | example ΔGf°, kJ mol–1 |
|---|---|
| O2(g) | O3(g) ΔGf° = 163.2 |
| C(graphite) | C(diamond) ΔGf° = 2.9 |
| S(rhombic) | S(monoclinic) ΔGf° = 0.1 |
| P(white) | P4(s) ΔGf° = 24.4 |
Ions in aqueous solution are a special case; their standard free energies are relative to the hydrated hydrogen ion H+(aq) which is assigned ΔGf° = 0.
Plain-vanilla ΔG is very different from ΔG° !
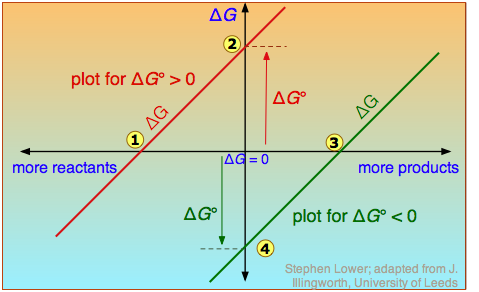
The distinction is nicely illustrated in this diagram in which ΔG is plotted on a vertical axis for two hypothetical reactions having opposite signs of ΔG°. The horizontal axis schematically expresses the relative concentrations of reactants and products at any point of the process. Note that the origin corresponds to the composition at which half of the reactants have been converted into products.
Take careful note of the following:
- The red line on the left plots the values of ΔG for the ΔG° > 0 reaction. Notice that there are an infinite number of these values, depending on the progress of the reaction. In contrast there is only a single value
 of ΔG°, corresponding to the composition at which ΔG = 0 (
of ΔG°, corresponding to the composition at which ΔG = 0 ( ).
). - At this point, some products have been formed, but the composition is still dominated by reactants.
- If we begin at a composition to the left of
 , ΔG will be negative and the composition will move to the right. Similarly if we begin with a composition to the right of
, ΔG will be negative and the composition will move to the right. Similarly if we begin with a composition to the right of  , ΔG will be positive and the composition will move to the left.
, ΔG will be positive and the composition will move to the left. - The plot on the right is for the ΔG° < 0 reaction, for which ΔG° is shown at
 . At its equilibrium point
. At its equilibrium point  , there are more products than reactants. If we start at a composition to the right of
, there are more products than reactants. If we start at a composition to the right of  , the composition will tend to move to the left. If the initial composition is to the left of
, the composition will tend to move to the left. If the initial composition is to the left of  , the reaction will tend to proceed to the right.
, the reaction will tend to proceed to the right. - What would happen if ΔG° were 0? The equilibrium point of such a reaction would be at the origin, corresponding to half the reactants being converted to products.
The important principle you should understand from this is that a negative ΔG° does not mean that the reactants will be completely transformed into products. By the same token, a positive ΔG° does not mean that no products are formed at all.
It should now be clear from the discussion above that a given reaction carried out under standard conditions is characterized by a single value of ΔG°.
In contrast, composition of a chemical reaction system undergoes continual change until the equilibrium state is reached. So the a single reaction can have an infinite number of ΔG values, reflecting the infinite possible compositions between the extremes of pure reactants (zero extent of reaction) and pure products (unity extent of reaction).
In the example of a reaction A → B, depicted in the above diagram, the standard free energy of the products ![]() is smaller than that of the reactants
is smaller than that of the reactants ![]() , so the reaction will take place spontaneously. But as will be explained in the next lesson, this does not mean that each mole of pure A will be converted into one mole of pure B. For reactions in which products and reactants occupy a single phase (gas or solution), the meaning of "spontaneous" is that the equilibrium composition
, so the reaction will take place spontaneously. But as will be explained in the next lesson, this does not mean that each mole of pure A will be converted into one mole of pure B. For reactions in which products and reactants occupy a single phase (gas or solution), the meaning of "spontaneous" is that the equilibrium composition ![]() will correspond to an extent of reaction greater than 0.5 but smaller than unity.
will correspond to an extent of reaction greater than 0.5 but smaller than unity.
The physical meaning of ΔG is that it tells us how far the free energy of the system has changed from G° of the pure reactants ![]() . As the reaction proceeds to the right, the composition changes, and ΔG begins to fall. When the composition reaches
. As the reaction proceeds to the right, the composition changes, and ΔG begins to fall. When the composition reaches ![]() , ΔG reaches its minimum value and further reaction would cause it to rise. But because free energy can only decrease but never increase, this does not happen. The composition of the system remains permanently at its equilibrium value.
, ΔG reaches its minimum value and further reaction would cause it to rise. But because free energy can only decrease but never increase, this does not happen. The composition of the system remains permanently at its equilibrium value.
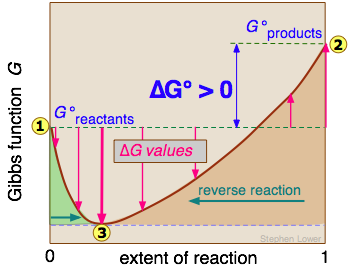 A G vs. extent-of-reaction diagram for a non-spontaneous reaction can be interpreted in a similar way; the equilibrium composition
A G vs. extent-of-reaction diagram for a non-spontaneous reaction can be interpreted in a similar way; the equilibrium composition ![]() will correspond to an extent of reaction greater than zero but less than 0.5.
will correspond to an extent of reaction greater than zero but less than 0.5.
In this case, the minimum at ![]() reflects the increase in entropy when the reactants are "contaminated" by a small quantity of products.
reflects the increase in entropy when the reactants are "contaminated" by a small quantity of products.
Some example processes
Although it is ΔG rather than ΔG° that serves as a criterion for spontaneous change at constant temperature and pressure, ΔG° values are so readily available that they are often used to get a rough idea of whether a given chemical change is possible. This is practical to do in some cases, but not in others.
It generally works for reactions such as
4 NH3(g)+ 5 O2(g)→ 4 NO(g)+ 6 H2O(g) ΔG° = –1010 kJ
(industrially important for the manufacture of nitric acid) because ΔG° is so negative that the reaction will be spontaneous and virtually complete under just about any reasonable set of conditions.
The following reaction expresses the fact that the water molecule is thermodynamically stable:
2 H2(g)+ ½ O2(g)→ H2O(g) ΔG° = –237.2 kJ
Note that this refers to liquid water (the standard state of H2O at 25°). If you think about it, a negative standard Gibbs energy of formation (of which this is an example) can in fact be considered a definition of molecular stability.
Similarly, dissociation of dihydrogen into its atoms is highly unlikely under standard conditions:
H2O(g)→ 2 H(g)+ O(g) ΔG° = +406.6 kJ
Again, an analogous situation would apply to any stable molecule.
Now consider the dissociation of dinitrogen tetroxide
N2O4(g)→ 2 NO2(g) ΔG° = +2.8 kJ
in which the positive value of ΔG° tells us that N2O4 at 1 atm pressure will not change into two moles of NO2 at the same pressure, but owing to the small absolute value of ΔG°, we can expect the spontaneity of the process to be quite sensitive to both the temperature (as shown in the table below) and to the pressure in exactly the way the Le Châtelier principle predicts.
For reactions involving dissolved ions, one has to be quite careful. Thus for the dissociation of the weak hydrofluoric acid
HF(aq) → H+(aq) + F–(aq) ΔG° = –317 kJ
it is clear that a 1 mol/L solution of HF will not dissociate into 1M ions, but this fact is not very useful because if the HF is added to water, the initial concentration of the fluoride ion will be zero (and that of H+ very close to zero), and the Le Châtelier principle again predicts that some dissociation will be spontaneous.
It is common knowledge that dissociation of water into hydrogen- and hydroxyl ions occurs only very sparingly:
H2O(l) → H+(aq) + OH–(aq) ΔG° = 79.9 kJ
which correctly predicts that the water will not form 1M (effective concentration) of the ions, but this is hardly news if you already know that the product of these ion concentrations can never exceed 10–14 at 298K.
Finally, consider this most familiar of all phase change processes, the vaporization of liquid water:
H2O(l)→ H2O(g) ΔG° = 8.58 kJ
Conversion of liquid water to its vapor at 1 atm partial pressure does not take place at 25° C, at which temperature the equiibrium partial pressure of the vapor (the "vapor pressure") is only 0.031 atm (23.8 torr.) Gaseous H2O at a pressure of 1 atm can only exist at 100° C. Of course, water left in an open container at room temperature will spontaneously evaporate if the partial pressure of water vapor in the air is less than 0.031 atm, corresponding to a relative humidity of under 100%
Finding the equilibrium temperature
A reaction is in its equilibrium state when
ΔG = ΔH – TΔS = 0
The temperature at which this occurs is given by
T = ΔH / TΔS (4-4)
If we approximate ΔH by ΔH° and ΔS by ΔS°, we can estimate the normal boiling point of a liquid. From the following thermodynamic data for water:
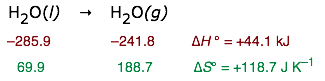
we find that liquid water is in equilibrium with water vapor at a partial pressure of 1 atm when the temperature is
T = (44100 J) / (118.7 J K–1) = 371.5 K
Of course, the farther one gets from 298K, the more unreliable will be the result. Thus for the dissociation of dihydrogen into its atoms,
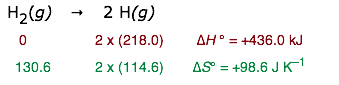
T = (436000 J) / (98.6 J K–1) = 4420 K
All one can say here is that H2 will break down at somethng over 3000K or so. (You may already know that all molecules will dissociate into their atoms at high temperatures.)
We tend to think of high temperatures as somehow "forcing" molecules to dissociate into their atoms, but this is wrong. In order to get the H–H bond to vibrate so violently through purely thermal excitation that the atoms would fly apart, a temperature more like 30,000K would be required. The proper interpretation is at the temperature corresponding to ΔH/TΔS, the molecule spontaneously absorbs energy from the surroundings sufficient to overcome the H-H bond strength.
Predicting the effects of temperature
In a previous section of this lesson we described the role of temperature in the Gibbs function, showed plots that explain how the sign of the TΔS term interacts with that of ΔH to determine whether the reaction can take place at a given temperature.
This can be more clearly understood by examining plots of TΔS° and ΔH° as functions of the temperature for some actual reactions. Of course these parameters refer to standard states that generally do not correspond to the temperatures, pressures, or concentrations that might be of interest in an actual case. Nevertheless, these quantities are easily found and they can usefully predict the way that temperature affects these systems.
Exothermic reaction, ΔS° > 0
|
C(graphite) + O2(g)→ CO2(g) ΔH° = –393 kJ
ΔS° = +2.9 J K–1, |
Exothermic reaction, ΔS° < 0
|
3 H2 + N2 → 2 NH3(g)
ΔH° = –46.2 kJ,
ΔS° = –389 J K–1, ΔG° = –16.4 kJ at 298 K. The decrease in moles of gas in the Haber ammonia synthesis drives the entropy change negative, making the reaction spontaneous only at low temperatures. Thus higher T, which speeds up the reaction, also reduces its extent. |
Endothermic reaction, ΔS° > 0
|
N2O4(g)→ 2 NO2(g),
ΔH° = 55.3 kJ,
ΔS° = +176 J K–1
ΔG° = +2.8 kJ at 298 K. Dissociation reactions are typically endothermic with positive entropy change, and are therefore spontaneous at high temperatures. Ultimately, all molecules decompose to their atoms at sufficiently high temperatures. |
Endothermic reaction, ΔS° < 0
|
½ N2 + O2 → NO2(g)
ΔH° = 33.2 kJ
ΔS° = –249 J K–1, ΔG° = +51.3 kJ at 298 K. This reaction is not spontaneous at any temperature, meaning that its reverse is always spontaneous. But because the reverse reaction is kinetically inhibited, NO2 can exist indefinitely at ordinary temperatures even though it is thermodynamically unstable. |
Free energy: is it free? Is it energy? Is it real?
It's not necessarily "free"
The appellation “free energy” for G has led to so much confusion that many scientists now refer to it simply as the Gibbs energy. The “free” part of the older name reflects the steam-engine origins of thermodynamics with its interest in converting heat into work: ΔG is the maximum amount of energy which can be “freed” from the system to perform useful work.
By "useful", we mean work other than that which is associated with the expansion of the system. This is most commonly in the form of electrical work (moving electric charge through a potential difference), but other forms of work (osmotic work, increase in surface area) are also possible.
It's not energy!
A much more serious difficulty with the Gibbs function, particularly in the context of chemistry, is that although G has the units of energy (joules, or in its intensive form, J mol–1), it lacks one of the most important attributes of energy in that it is not conserved. Thus although the free energy always falls when a gas expands or a chemical reaction takes place spontaneously, there need be no compensating increase in energy anywhere else. Referring to G as an energy also reinforces the false but widespread notion that a fall in energy must accompany any change. But if we accept that energy is conserved, it is apparent that the only necessary condition for change (whether the dropping of a weight, expansion of a gas, or a chemical reaction) is the redistribution of energy. The quantity –ΔG associated with a process represents the quantity of energy that is “shared and spread”, which as we have already explained is the meaning of the increase in the entropy. The quotient –ΔG/T is in fact identical with ΔStotal, the entropy change of the world, whose increase is the primary criterion for any kind of change.
It's not even "real"!
G differs from the thermodynamic quantities H and S in another significant way: it has no physical reality as a property of matter, whereas H and S can be related to the quantity and distribution of energy in a collection of molecules. The free energy is simply a useful construct that serves as a criterion for change and makes calculations easier.
Who was Gibbs, anyway?
J. Willard Gibbs (1839-1903) is considered the father of modern thermodynamics and the most brilliant American-born scientist of the 19th century. He did most of his work in obscurity, publishing his difficult-to-understand papers in the Proceedings of the Connecticut Academy of Sciences, a little-read journal that was unknown to most of the world.
Some Gibbs links: brief bio - scientific biography. A remarkably rich account of Gibbs' seemingly gray life and his unusual powers of visualization was written by a noted American poet: M. Rukeyser, Willard Gibbs. Garden City, N.J.: Doubleday Duran and Co., Inc., 1942.
In order to keep this rather long page from getting even longer, this topic has its own separate page.
Please note, however, that this material is not normally covered in elementary Chemistry courses. So unless you are enrolled in a university-level honors course which makes explicit reference to this topic, you can safely skip it.
That having been said, this additional matierial is a natural extension of what is presented above and leads to a more complete understanding of chemical equilibrium. It is presented in a way that emphasizes the basic concepts and avoids the mathematical rigor of the standard physical chemistry treatment.
(You are expected to be able to define and explain the significance of terms identified in green type.)
- The Gibbs [free] energy is a state function defined as G = H – TS .
- The Gibbs energy is the maximum useful work that a system can do on the surroundings when the process occurs reversibly at constant temperature and pressure.
- The practical utility of the Gibbs function is that ΔG for any process is negative if it leads to an increase in the entropy of the world. Thus spontaneous change at a given temperature and pressure can only occur when it would lead to a decrease in G.
- The sign of the standard free energy change ΔG° of a chemical reaction determines whether the reaction will tend to proceed in the forward or reverse direction.
- Similarly, the relative signs of ΔG° and ΔS° determine whether the spontaniety of a chemical reaction will be affected by the temperature, and if so, in what way.
- The existence of sharp melting and boiling points reflects the differing temperature dependancies of the free energies of the solid, liquid, and vapor phases of a pure substance, which are in turn reflect their differing entropies.