From coins to molecules: why energy spreads
Disorder is more probable than order because there are so many more ways of achieving it. Thus coins and cards tend to assume random configurations when tossed or shuffled, and socks and books tend to become more scattered about a teenager’s room during the course of daily living. But there are some important differences between these large-scale mechanical, or macro systems, and the collections of sub-microscopic particles that constitute the stuff of chemistry.
- In systems of chemical interest we are dealing with huge numbers of particles.
- This is important because statistical predictions are always more accurate for larger samples. Thus although for four coin tosses there is a good chance (62%) that the H/T ratio will fall outside the range of 0.45 - 0.55, this probability becomes almost zero for 1000 tosses. To express this in a different way, the chances that 1000 gas molecules moving about randomly in a container would at any instant be distributed in a sufficiently non-uniform manner to produce a detectable pressure difference between any two halves of the space will be extremely small. If we increase the number of molecules to a chemically significant number (around 1020, say), then the same probability becomes indistinguishable from zero.
- Once the change begins, it proceeds spontaneously. That is, no external agent (a tosser, shuffler, or teen-ager) is needed to keep the process going. As long as the temperature is high enough for sufficiently energetic collisions to occur between the reacting molecules in a gas, the reaction will proceed to completion on its own once the reactants have been brought together.
- Thermal energy is continually being exchanged between the particles of the system, and between the system and the surroundings. Collisions between molecules result in exchanges of momentum (and thus of kinetic energy) amongst the particles of the system, and (through collisions with the walls of a container, for example) with the surroundings.
- Thermal energy spreads rapidly and randomly throughout the various energetically accessible microstates of the system. The degree to which the thermal energy is dispersed amongst these microstates is known as the entropy of the system.
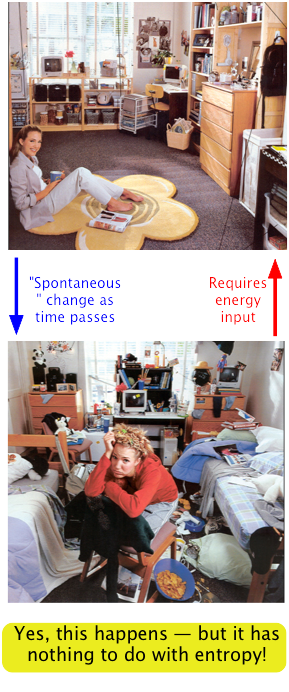
Don't make the mistake of equating entropy with "disorder"!
This very common error has unfortunately made it's way into the popular culture:
→
How thermal energy is stored in molecules
When a collection of molecules absorbs thermal energy, it increases their average kinetic energies, and thus their temperature. The actual motions that constitute a molecule's kinetic energy are of three kinds:
- All molecules (even monatomic ones) will possess translational kinetic energy at all temperatures above absolute zero. In other words, the higher the temperature, the faster they move.
- Molecules containing two or more atoms can also possess kinetic energies associated with internal vibrations such as the stretching and bending of bonds.
- Finally, polyatomic molecules that are free to do so (as in gases) can divert some of their kinetic energy into rotational motions.
In general, the more atoms in the molecule and the more complicated it's structure, the more of these microstates there are, and the more energy it can store.
In order to understand how a molecule's kinetic energy is distributed amongst these three kinds of motions, you must understand that at the atomic and molecular level, all energy is quantized; each particle possesses discrete states of kinetic energy and is able to accept thermal energy only in packets whose values correspond to the energies of one or more of these states.
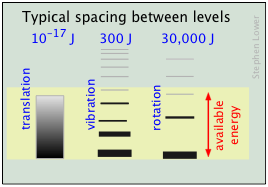 ← The relative populations of the quantized translational, rotational and vibrational energy states of a typical diatomic molecule are depicted by the thickness of the lines in this schematic (not-to-scale!) diagram. The colored shading indicates the total thermal energy available at an arbitrary temperature. The numbers at the top show order-of-magnitude spacings between adjacent levels.
← The relative populations of the quantized translational, rotational and vibrational energy states of a typical diatomic molecule are depicted by the thickness of the lines in this schematic (not-to-scale!) diagram. The colored shading indicates the total thermal energy available at an arbitrary temperature. The numbers at the top show order-of-magnitude spacings between adjacent levels.
Notice that the spacing between the quantized translational levels is so minute that they can be considered nearly continuous. This means that at all temperatures, the thermal energy of a collection of molecules resides almost exclusively in translational microstates. At ordinary temperatures (around 25° C), most of the molecules are in their zero-level vibrational and rotational states (corresponding to the bottom-most bars in the diagram.) The prevalence of vibrational states is so overwhelming that we can effectively equate the thermal energy of molecules with translational motions alone.
The number of ways in which thermal energy can be distributed amongst the allowed states within a collection of molecules is easily calculated from simple statistics. A very important point to bear in mind is that the number of discrete microstates that can be populated by an arbitrary quantity of energy depends on the spacing of the states. As a very simple example, suppose that we have two molecules (depicted by the orange dots) in a system total available thermal energy is indicated by the yellow shading:
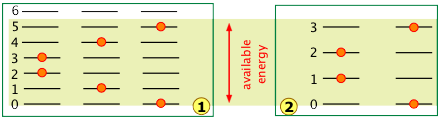
In system ![]() , the same quantity of energy is sufficient produce three microstates in which the two molecules are distributed over the quantized levels 0 through 5.
, the same quantity of energy is sufficient produce three microstates in which the two molecules are distributed over the quantized levels 0 through 5.
Owing to the wider spacing of the quantum levels in system ![]() , fewer quantum levels are accessible, yielding only two possible microstates.
, fewer quantum levels are accessible, yielding only two possible microstates.
It's actually a bit more complicated than this, because simple exchange of molecules between the same two levels increases the number of microstates. Suppose that we have a system consisting of three molecules and three quanta of energy to share among them. We can give all the kinetic energy to any one molecule, leaving the others with none, we can give two units to one molecule and one unit to another, or we can share out the energy equally and give one unit to each molecule. All told, there are ten possible ways of distributing three units of energy among three identical molecules as shown here:
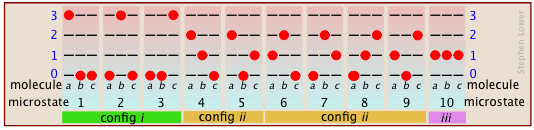
As the number of molecules and the number of quanta increases, the number of accessible microstates grows explosively; if 1000 quanta of energy are shared by 1000 molecules, the number of available microstates will be around 10600— a number that greatly exceeds the number of atoms in the observable universe! The number of possible configurations (as defined above) also increases, but in such a way as to greatly reduce the probability of all but the most probable configurations. Thus for a sample of a gas large enough to be observable under normal conditions, only a single configuration (energy distribution amongst the quantum states) need be considered; even the second-most-probable configuration can be neglected.
The bottom line: any collection of molecules large enough in numbers to have chemical significance will have its therrmal energy distributed over an unimaginably large number of microstates. The number of microstates increases exponentially as more energy states ("configurations" as defined above) become accessible owing to
- Addition of energy quanta (higher temperature),
- Increase in the number of molecules (resulting from dissociation, for example).
- the volume of the system increases (which decreases the spacing between energy states, allowing more of them to be populated at a given temperature.)
Energy-spreading changes the world
Energy is conserved; if you lift a book off the table, and let it fall, the total amount of energy in the world remains unchanged. All you have done is transferred it from the form in which it was stored within the glucose in your body to your muscles, and then to the book (that is, you did work on the book by moving it up against the earth’s gravitational field.) After the book has fallen, this same quantity of energy exists as thermal energy (heat) in the book and table top.
What has changed, however, is the availability of this energy. Once the energy has spread into the huge number of thermal microstates in the warmed objects, the probabiliy of its spontaneously (that is, by chance) becoming un-dispersed is essentially zero. Thus although the energy is still “there”, it is forever beyond utilization or recovery.
The profundity of this conclusion was recognized around 1900, when it was first described at the “heat death” of the world. This refers to the fact that every spontaneous process (essentially every change that occurs) is accompanied by the “dilution” of energy. The obvious implication is that all of the molecular-level kinetic energy will be spread out completely, and nothing more will ever happen. Not a happy thought!
Why do gases tend to expand but never contract?
Everybody knows that a gas, if left to itself, will tend to expand and fill the volume within which it is confined completely and uniformly. What “drives” this expansion? At the simplest level it is clear that with more space available, random motions of the individual molecules will inevitably disperse them throughout the space. But as we mentioned above, the allowed energy states that molecules can occupy are spaced more closely in a larger volume than in a smaller one. The larger the volume available to the gas, the greater the number of microstates its thermal energy can occupy. Since all such states within the thermally accessible range of energies are equally probable, the expansion of the gas can be viewed as a consequence of the tendency of thermal energy to be spread and shared as widely as possible. Once this has happened, the probability that this sharing of energy will reverse itself (that is, that the gas will spontaneously contract) is so minute as to be unthinkable.
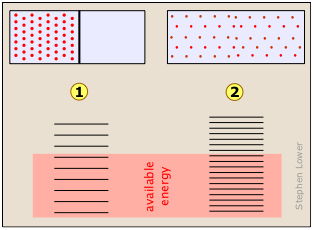 Imagine a gas initially confined to one half of a box, as shown at
Imagine a gas initially confined to one half of a box, as shown at ![]() . We then remove the barrier so that it can expand into the full volume of the container (
. We then remove the barrier so that it can expand into the full volume of the container (![]() .) In its expanded, lower-pressure state, the allowed translational microstates of the gas are more closely spaced. Because more microstates are energetically accessible to the gas molecules in
.) In its expanded, lower-pressure state, the allowed translational microstates of the gas are more closely spaced. Because more microstates are energetically accessible to the gas molecules in ![]() than in
than in ![]() , the additional microstates are quickly populated.
, the additional microstates are quickly populated.
In other words, the configuration of the system corresponding to the expanded state of the gas is so massively more probable than the initial state (because there are so many more ways of realizing it) that probability of the reverse process ![]() →
→ ![]() is vanishingly small.
is vanishingly small.
Entropy of mixing and dilution
The expansion process described above can also be thought of as a kind of "dilution". Mixing and dilution really amount to the same thing, especially for gases that approach ideal behavior.
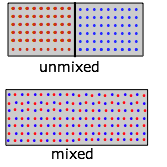 Replace the pair of containers shown in the expansion diagram with one containing two kinds of molecules in the separate sections. When we remove the barrier, the "red" and "blue" molecules will each expand into the space of the other. (Recall Dalton's Law that "each gas is a vacuum to the other gas".) But notice that although each gas underwent an expansion, the overall process amounts to what we call "mixing".
Replace the pair of containers shown in the expansion diagram with one containing two kinds of molecules in the separate sections. When we remove the barrier, the "red" and "blue" molecules will each expand into the space of the other. (Recall Dalton's Law that "each gas is a vacuum to the other gas".) But notice that although each gas underwent an expansion, the overall process amounts to what we call "mixing".
What is true for gaseous molecules can, in principle, apply also to solute molecules dissolved in a solvent. But bear in mind that whereas the enthalpy associated with the expansion of a perfect gas is by definition zero, ΔH's of mixing of two liquids or of dissolving a solute in a solvent have finite values which may limit the miscibility of liquids or the solubility of a solute.
It's unfortunate the the simplified diagrams we are using to illustrate the greater numbers of energetically accessible microstates in an expanded gas or a mixture of gases fail to convey the immensity of this increase. Only by working through the statistical mathematics of these processes (thankfully beyond the scope of first-year Chemistry!) can one gain an appreciation of the magnitude of the probabilities of these spontaneous processes.
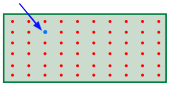
It turns out that when just one molecule of a second gas is inroduced into the container of another gas, an unimaginably huge number of new configurations becom available. This happens because the added molecule (indicated by the blue arrow in the diagram) can in principle replace any one of the old (red) ones, each case giving rise to a new microstate.
Why heat flows from hot to cold
J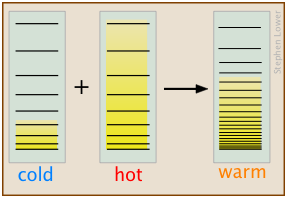 ust as gases spontaneously change their volumes from “smaller-to-larger”, the flow of heat from a warmer body to a cooler one always operates in the direction “warmer-to-cooler” because this allows thermal energy to populate a larger number of energy microstates as new ones are made available by bringing the cooler body into contact with the warmer one; in effect, the thermal energy becomes more “diluted”. In this simplified schematic diagram, the "cold" and "hot" bodies differ in the numbers of translational microstates that are occupied, as indicated by the shading. When they are brought into thermal contact, a hugely greater number of microstates are created, as is indicated by their closer spacing in the rightmost section of the diagram, which represents the combined bodies in thermal equilibrium. The thermal energy in the initial two bodies fills these new microstates to a level (and thus, temperature) that is somewhere between those of the two original bodies.
ust as gases spontaneously change their volumes from “smaller-to-larger”, the flow of heat from a warmer body to a cooler one always operates in the direction “warmer-to-cooler” because this allows thermal energy to populate a larger number of energy microstates as new ones are made available by bringing the cooler body into contact with the warmer one; in effect, the thermal energy becomes more “diluted”. In this simplified schematic diagram, the "cold" and "hot" bodies differ in the numbers of translational microstates that are occupied, as indicated by the shading. When they are brought into thermal contact, a hugely greater number of microstates are created, as is indicated by their closer spacing in the rightmost section of the diagram, which represents the combined bodies in thermal equilibrium. The thermal energy in the initial two bodies fills these new microstates to a level (and thus, temperature) that is somewhere between those of the two original bodies.
Note that this explanation applies equally well to the case of two solids brought into thermal contact, or to the mixing of two fluids having different temperatures.
As you might expect, the increase in the amount of energy spreading and sharing, and thus the entropy, is proportional to the amount of heat transferred q, but there is one other factor involved, and that is the temperature at which the transfer occurs. When a quantity of heat q passes into a system at temperature T, the degree of dilution of the thermal energy is given by
q /T
To understand why we have to divide by the temperature, consider the effect of very large and very small values of T in the denominator. If the body receiving the heat is initially at a very low temperature, relatively few thermal energy states are initially occupied, so the amount of energy spreading into vacant states can be very great. Conversely, if the temperature is initially large, more thermal energy is already spread around within it, and absorption of the additional energy will have a relatively small effect on the degree of thermal disorder within the body.
Chemical reactions: why the equilibrium constant depends on the temperature
When a chemical reaction takes place, two kinds of changes relating to thermal energy are involved:
- The ways that thermal energy can be stored within the reactants will generally be different from those for the products. For example, in the reaction H2→ 2 H, the reactant dihydrogen possesses vibrational and rotational energy states, while the atomic hydrogen in the product has translational states only— but the total number of translational states in two moles of H is twice as great as in one mole of H2. Because of their extremely close spacing, translational states are the only ones that really count at ordinary temperatures, so we can say that thermal energy can become twice as diluted (“spread out”) in the product than in the reactant. If this were the only factor to consider, then dissociation of dihydrogen would always be spontaneous and this molecule would not exist.
- In order for this dissociation to occur, however, a quantity of thermal energy (heat) q =ΔU must be taken up from the surroundings in order to break the H–H bond. In other words, the ground state (the energy at which the manifold of energy states begins) is higher in H, as indicated by the vertical displacement of the right half in each of the four panels below.
Shown below are schematic representations of the translational energy levels of the two components H and H2 of the hydrogen dissociation reaction. The shading shows how the relative populations of occupied microstates vary with the temperature, causing the equilibrium composition to change in favor of the dissociation product.
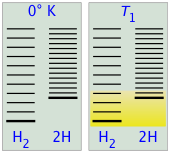
The ability of energy to spread into the product molecules is constrained by the availability of sufficient thermal energy to produce these molecules. This is where the temperature comes in. At absolute zero the situation is very simple; no thermal enegy is available to bring about dissociation, so the only component present will be dihydrogen.
- As the temperature increases, the number of populated energy states rises, as indicated by the shading in the diagram. At temperature T1, the number of populated states of H2 is greater than that of 2H, so some of the latter will be present in the equilibrium mixture, but only as the minority component.
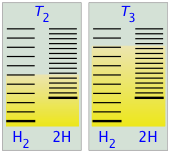
- At some temperature T2 the numbers of populated states in the two components of the reaction system will be identical, so the equilibrium mixture will contain H2 and “2H” in equal amounts; that is, the mole ratio of H2/H will be 1:2.
- As the temperature rises to T3 and above, we see that the number of energy states that are thermally accessible in the product begins to exceed that for the reactant, thus favoring dissociation.
The result is exactly what the LeChâtelier Principle predicts: the equilibrium state for an endothermic reaction is shifted to the right at higher temperatures.
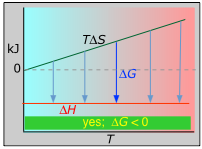
The following four panels illustrate these relations for the four possible sign-combinations of ΔH and ΔS.
Please take the time to understand each of these examples, taking special note of the plots of ΔH vs T for each case. (Asking students to construct and interpret one of these plots for a reaction having given values of ΔH and ΔS is a commen exam question in university-level courses, so be warned!)
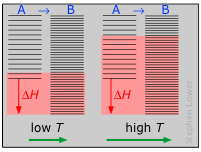
The other plot (which can safely be ignored by non-enthusiasts) attempts to illustrate the relative numbers of translational microstates that are accessible to each system at low and high temperatures.
Here we go!
Example 1: ΔH negative, ΔS positive; C(graphite) + O2(g) → CO2(g)
ΔH° = –393 kJ
ΔS° = +2.9 J K–1
ΔG° = –394 kJ at 298 K
This combustion reaction, like most such reactions, is spontaneous at all temperatures. The positive entropy change is due mainly to the greater mass of CO2 molecules compared to those of O2.
Example 2: ΔH and ΔS both negative; 3 H2 + N2 → 2 NH3(g)
ΔH° = –46.2 kJ
ΔS° = –389 J K–1
ΔG° = –16.4 kJ at 298 K
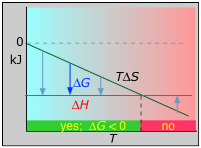
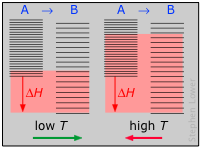
The decrease in moles of gas in the products drives the entropy change negative, making the reaction spontaneous only at low temperatures.
Example 3: ΔH and ΔS both positive; N2O4(g) → 2 NO2(g)
ΔH° = 55.3 kJ
ΔS° = +176 J K–1
ΔG° = +2.8 kJ at 298 K
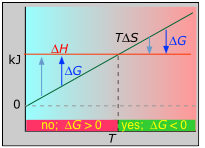
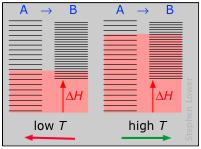
Dissociation reactions are typically endothermic with positive entropy change, and are therefore spontaneous at high temperatures. Ultimately, all molecules decompose to their atoms at sufficiently high temperatures.
Example 4: ΔH positive, ΔS negative; N2 + 2 O2 → 2 NO2(g)
ΔH° = 33.2 kJ
ΔS° = –249 J K–1
ΔG° = +51.3 kJ at 298 K
This reaction is not spontaneous at any temperature, meaning that its reverse is always spontaneous. But because the reverse reaction is kinetically inhibited, NO2 can exist indefinitely at ordinary temperatures even though it is thermodynamically unstable.